Menu Close

Question-167202

Tinku Tara 0 Comments
Pin




Question Number 167202 by DAVONG last updated on 09/Mar/22
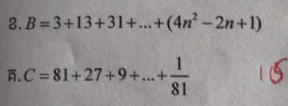
Answered by Rasheed.Sindhi last updated on 09/Mar/22
B=3+13+31+...+(4n^2 −2n+1) B=Σ_(n=1) ^n (4n^2 −2n+1) =4Σ_(n=1) ^(n) n^2 −2Σ_(n=1) ^(n) n+Σ_(n=1) ^(n) 1 =4(((n(n+1)(2n+1))/6))−2(((n(n+1))/2))+n =((2n(n+1)(2n+1)−3n(n+1)+3n)/3) =((n(n+1){2(2n+1)−3}+3n)/3) =((n(n+1)(4n−1)+3n)/3) =((n{(n+1)(4n−1)+3})/3) =((n(4n^2 +3n+2))/3)
$$\mathrm{B}=\mathrm{3}+\mathrm{13}+\mathrm{31}+…+\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$\mathrm{B}=\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$=\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{{n}} {\Sigma}}{n}^{\mathrm{2}} −\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{{n}} {\Sigma}}{n}+\underset{{n}=\mathrm{1}} {\overset{{n}} {\Sigma}}\mathrm{1} \\ $$$$=\mathrm{4}\left(\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\right)−\mathrm{2}\left(\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right)+{n} \\ $$$$=\frac{\mathrm{2}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{3}{n}\left({n}+\mathrm{1}\right)+\mathrm{3}{n}}{\mathrm{3}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left\{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{3}\right\}+\mathrm{3}{n}}{\mathrm{3}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{4}{n}−\mathrm{1}\right)+\mathrm{3}{n}}{\mathrm{3}} \\ $$$$=\frac{{n}\left\{\left({n}+\mathrm{1}\right)\left(\mathrm{4}{n}−\mathrm{1}\right)+\mathrm{3}\right\}}{\mathrm{3}} \\ $$$$=\frac{{n}\left(\mathrm{4}{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}\right)}{\mathrm{3}} \\ $$
Answered by Rasheed.Sindhi last updated on 10/Mar/22
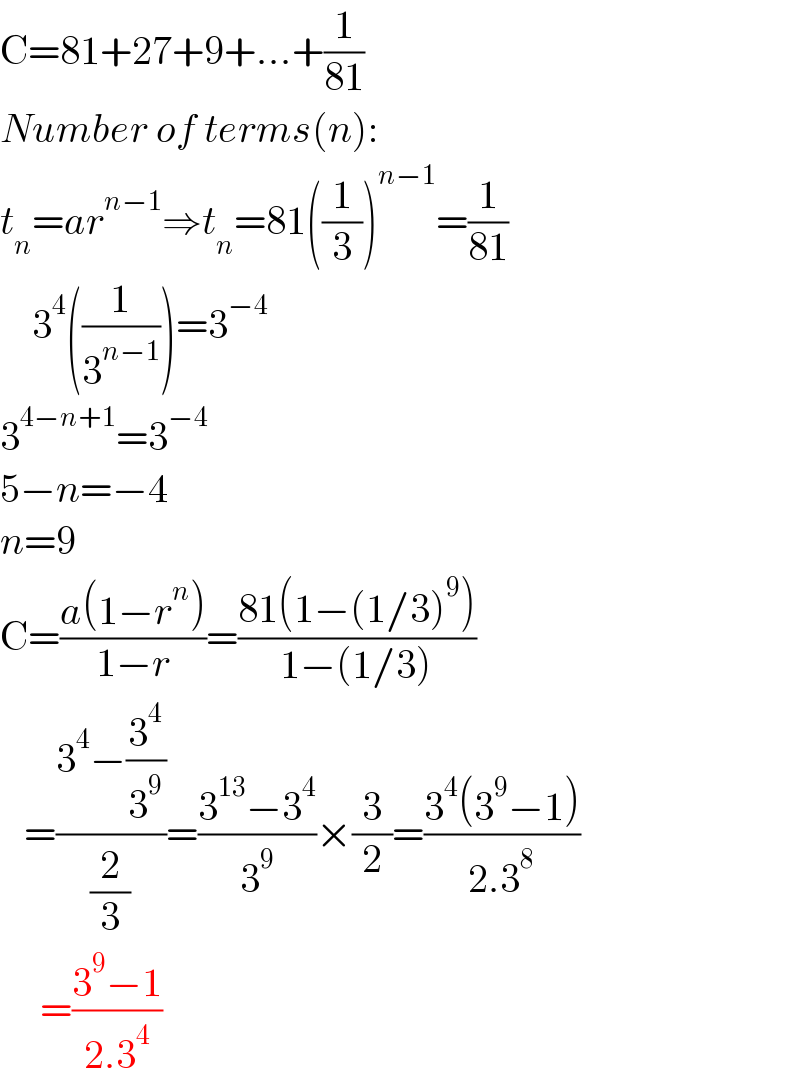
C=81+27+9+...+(1/(81)) Number of terms(n): t_n =ar^(n−1) ⇒t_n =81((1/3))^(n−1) =(1/(81)) 3^4 ((1/3^(n−1) ))=3^(−4) 3^(4−n+1) =3^(−4) 5−n=−4 n=9 C=((a(1−r^n ))/(1−r))=((81(1−(1/3)^9 ))/(1−(1/3))) =((3^4 −(3^4 /3^9 ))/(2/3))=((3^(13) −3^4 )/3^9 )×(3/2)=((3^4 (3^9 −1))/(2.3^8 )) =((3^9 −1)/(2.3^4 ))
$$\mathrm{C}=\mathrm{81}+\mathrm{27}+\mathrm{9}+…+\frac{\mathrm{1}}{\mathrm{81}} \\ $$$${Number}\:{of}\:{terms}\left({n}\right): \\ $$$${t}_{{n}} ={ar}^{{n}−\mathrm{1}} \Rightarrow{t}_{{n}} =\mathrm{81}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{81}} \\ $$$$\:\:\:\:\mathrm{3}^{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{3}^{{n}−\mathrm{1}} }\right)=\mathrm{3}^{−\mathrm{4}} \\ $$$$\mathrm{3}^{\mathrm{4}−{n}+\mathrm{1}} =\mathrm{3}^{−\mathrm{4}} \\ $$$$\mathrm{5}−{n}=−\mathrm{4} \\ $$$${n}=\mathrm{9} \\ $$$$\mathrm{C}=\frac{{a}\left(\mathrm{1}−{r}^{{n}} \right)}{\mathrm{1}−{r}}=\frac{\mathrm{81}\left(\mathrm{1}−\left(\mathrm{1}/\mathrm{3}\right)^{\mathrm{9}} \right)}{\mathrm{1}−\left(\mathrm{1}/\mathrm{3}\right)} \\ $$$$\:\:\:=\frac{\mathrm{3}^{\mathrm{4}} −\frac{\mathrm{3}^{\mathrm{4}} }{\mathrm{3}^{\mathrm{9}} }}{\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\mathrm{3}^{\mathrm{13}} −\mathrm{3}^{\mathrm{4}} }{\mathrm{3}^{\mathrm{9}} }×\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{3}^{\mathrm{4}} \left(\mathrm{3}^{\mathrm{9}} −\mathrm{1}\right)}{\mathrm{2}.\mathrm{3}^{\mathrm{8}} } \\ $$$$\:\:\:\:\:=\frac{\mathrm{3}^{\mathrm{9}} −\mathrm{1}}{\mathrm{2}.\mathrm{3}^{\mathrm{4}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *