Menu Close

solve-I-0-1-2-ln-2-x-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 167213 by mnjuly1970 last updated on 09/Mar/22
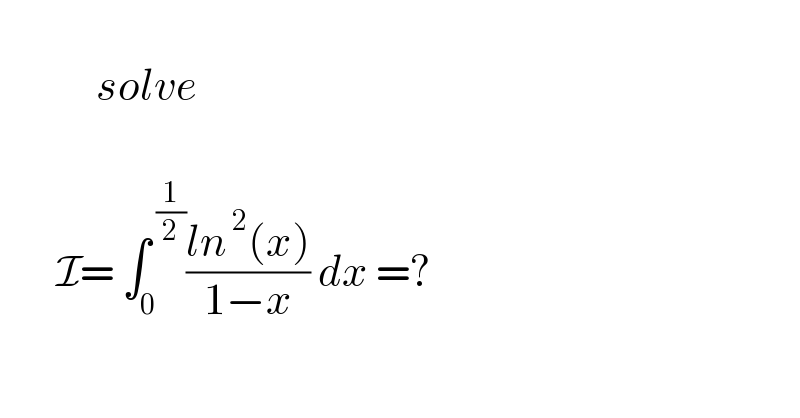
solve I= ∫_0 ^( (1/2)) ((ln^( 2) (x))/(1−x)) dx =?
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{solve} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\mathcal{I}=\:\int_{\mathrm{0}} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}^{\:\mathrm{2}} \left({x}\right)}{\mathrm{1}−{x}}\:{dx}\:=? \\ $$$$ \\ $$
Answered by mindispower last updated on 10/Mar/22
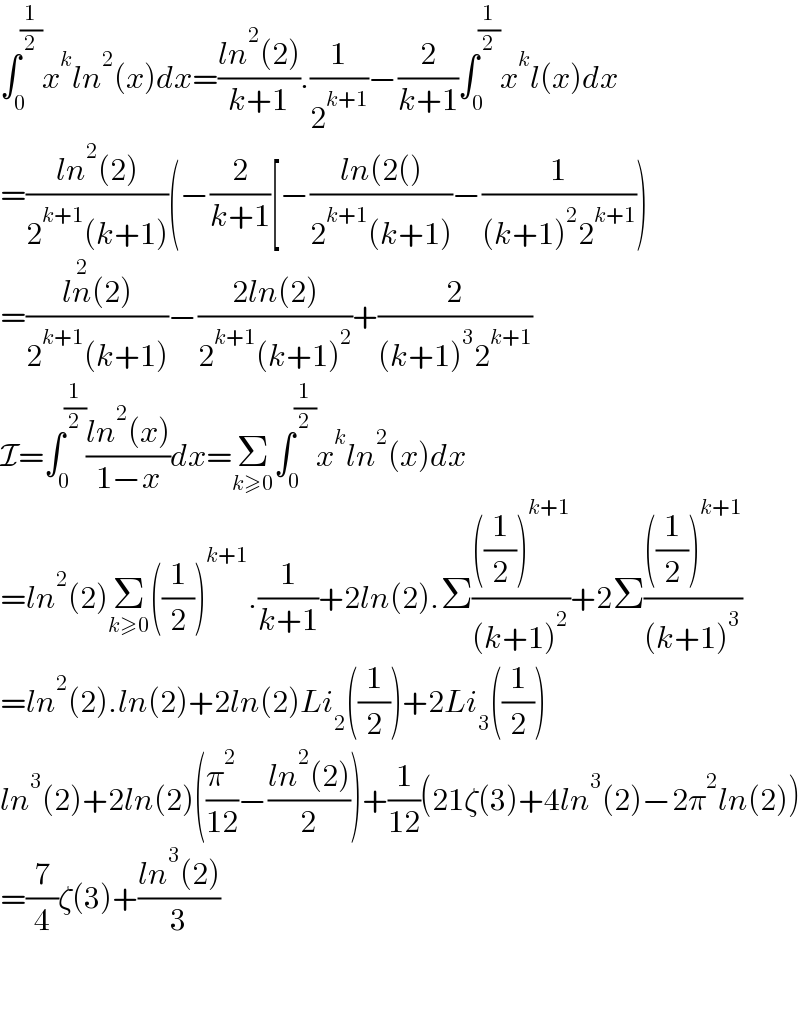
∫_0 ^(1/2) x^k ln^2 (x)dx=((ln^2 (2))/(k+1)).(1/2^(k+1) )−(2/(k+1))∫_0 ^(1/2) x^k l(x)dx =((ln^2 (2))/(2^(k+1) (k+1)))(−(2/(k+1))[−((ln(2())/(2^(k+1) (k+1)))−(1/((k+1)^2 2^(k+1) ))) =((ln^2 (2))/(2^(k+1) (k+1)))−((2ln(2))/(2^(k+1) (k+1)^2 ))+(2/((k+1)^3 2^(k+1) )) I=∫_0 ^(1/2) ((ln^2 (x))/(1−x))dx=Σ_(k≥0) ∫_0 ^(1/2) x^k ln^2 (x)dx =ln^2 (2)Σ_(k≥0) ((1/2))^(k+1) .(1/(k+1))+2ln(2).Σ((((1/2))^(k+1) )/((k+1)^2 ))+2Σ((((1/2))^(k+1) )/((k+1)^3 )) =ln^2 (2).ln(2)+2ln(2)Li_2 ((1/2))+2Li_3 ((1/2)) ln^3 (2)+2ln(2)((π^2 /(12))−((ln^2 (2))/2))+(1/(12))(21ζ(3)+4ln^3 (2)−2π^2 ln(2)) =(7/4)ζ(3)+((ln^3 (2))/3)
$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{{k}} {ln}^{\mathrm{2}} \left({x}\right){dx}=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{{k}+\mathrm{1}}.\frac{\mathrm{1}}{\mathrm{2}^{{k}+\mathrm{1}} }−\frac{\mathrm{2}}{{k}+\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{{k}} {l}\left({x}\right){dx} \\ $$$$=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}^{{k}+\mathrm{1}} \left({k}+\mathrm{1}\right)}\left(−\frac{\mathrm{2}}{{k}+\mathrm{1}}\left[−\frac{{ln}\left(\mathrm{2}\left(\right)\right.}{\mathrm{2}^{{k}+\mathrm{1}} \left({k}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{2}^{{k}+\mathrm{1}} }\right)\right. \\ $$$$=\frac{{l}\overset{\mathrm{2}} {{n}}\left(\mathrm{2}\right)}{\mathrm{2}^{{k}+\mathrm{1}} \left({k}+\mathrm{1}\right)}−\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{2}^{{k}+\mathrm{1}} \left({k}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\left({k}+\mathrm{1}\right)^{\mathrm{3}} \mathrm{2}^{{k}+\mathrm{1}} } \\ $$$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}−{x}}{dx}=\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{{k}} {ln}^{\mathrm{2}} \left({x}\right){dx} \\ $$$$={ln}^{\mathrm{2}} \left(\mathrm{2}\right)\underset{{k}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{k}+\mathrm{1}} .\frac{\mathrm{1}}{{k}+\mathrm{1}}+\mathrm{2}{ln}\left(\mathrm{2}\right).\Sigma\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{k}+\mathrm{1}} }{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{2}\Sigma\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{k}+\mathrm{1}} }{\left({k}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$={ln}^{\mathrm{2}} \left(\mathrm{2}\right).{ln}\left(\mathrm{2}\right)+\mathrm{2}{ln}\left(\mathrm{2}\right){Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}{Li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${ln}^{\mathrm{3}} \left(\mathrm{2}\right)+\mathrm{2}{ln}\left(\mathrm{2}\right)\left(\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{21}\zeta\left(\mathrm{3}\right)+\mathrm{4}{ln}^{\mathrm{3}} \left(\mathrm{2}\right)−\mathrm{2}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)\right) \\ $$$$=\frac{\mathrm{7}}{\mathrm{4}}\zeta\left(\mathrm{3}\right)+\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 10/Mar/22
thank you so much sir power...
$$\:\:\:\:{thank}\:{you}\:{so}\:{much}\:{sir} \\ $$$$\:\:\:{power}… \\ $$
Commented by mindispower last updated on 10/Mar/22
Withe Pleasur sir Have a nice Day
$${Withe}\:{Pleasur}\:{sir} \\ $$$${Have}\:{a}\:{nice}\:{Day} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *