Question Number 167220 by tabata last updated on 09/Mar/22

Answered by MikeH last updated on 10/Mar/22
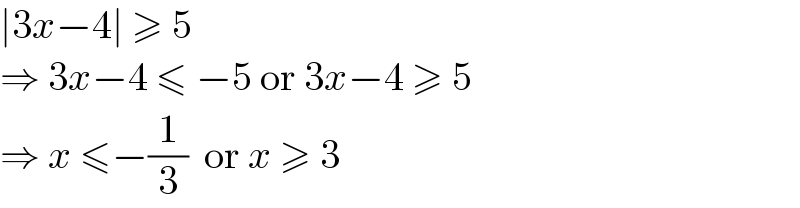
$$\mid\mathrm{3}{x}−\mathrm{4}\mid\:\geqslant\:\mathrm{5} \\ $$$$\Rightarrow\:\mathrm{3}{x}−\mathrm{4}\:\leqslant\:−\mathrm{5}\:\mathrm{or}\:\mathrm{3}{x}−\mathrm{4}\:\geqslant\:\mathrm{5} \\ $$$$\Rightarrow\:{x}\:\leqslant−\frac{\mathrm{1}}{\mathrm{3}}\:\:\mathrm{or}\:{x}\:\geqslant\:\mathrm{3} \\ $$
Answered by MikeH last updated on 10/Mar/22
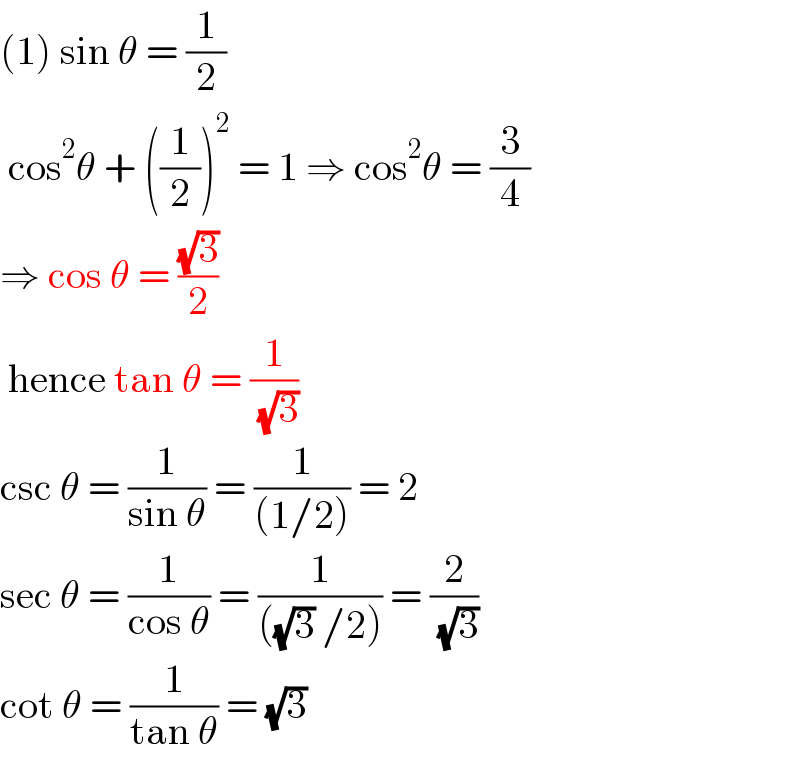
$$\left(\mathrm{1}\right)\:\mathrm{sin}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\:\mathrm{cos}^{\mathrm{2}} \theta\:+\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:=\:\mathrm{1}\:\Rightarrow\:\mathrm{cos}^{\mathrm{2}} \theta\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\mathrm{hence}\:\mathrm{tan}\:\theta\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{csc}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{sin}\:\theta}\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}/\mathrm{2}\right)}\:=\:\mathrm{2} \\ $$$$\mathrm{sec}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:\theta}\:=\:\frac{\mathrm{1}}{\left(\sqrt{\mathrm{3}}\:/\mathrm{2}\right)}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{cot}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{tan}\:\theta}\:=\:\sqrt{\mathrm{3}} \\ $$
