Question Number 134596 by mohammad17 last updated on 05/Mar/21

Commented by mohammad17 last updated on 05/Mar/21

$${help}\:{me}\:{sir} \\ $$
Answered by Olaf last updated on 05/Mar/21
![a) ∫_C (z+1)dz = ∫_0 ^1 (x+1+ix^2 )dx = [(x^2 /2)+x+i(x^3 /3)]_0 ^1 = (3/2)+(i/3) b) ∫_C (x^2 +iy^3 )dz = ∫_0 ^(√2) (rcos^2 (π/4)+ir^3 cos^3 (π/4))dr = [(r^2 /4)+i(r^4 /(8(√2)))]_0 ^(√2) = (1/2)+(i/( 2(√2))) c) ∫_C xdz = ∫_0 ^(2π) rcosθdθ = 0](https://www.tinkutara.com/question/Q134603.png)
$$\left.{a}\right) \\ $$$$\int_{\mathrm{C}} \left({z}+\mathrm{1}\right){dz}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}+\mathrm{1}+{ix}^{\mathrm{2}} \right){dx} \\ $$$$=\:\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{x}+{i}\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\frac{\mathrm{3}}{\mathrm{2}}+\frac{{i}}{\mathrm{3}} \\ $$$$\left.{b}\right) \\ $$$$\int_{\mathrm{C}} \left({x}^{\mathrm{2}} +{iy}^{\mathrm{3}} \right){dz} \\ $$$$=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \left({r}\mathrm{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{4}}+{ir}^{\mathrm{3}} \mathrm{cos}^{\mathrm{3}} \frac{\pi}{\mathrm{4}}\right){dr} \\ $$$$=\:\left[\frac{{r}^{\mathrm{2}} }{\mathrm{4}}+{i}\frac{{r}^{\mathrm{4}} }{\mathrm{8}\sqrt{\mathrm{2}}}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}}{\:\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\left.{c}\right) \\ $$$$\int_{\mathrm{C}} {xdz}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {r}\mathrm{cos}\theta{d}\theta\:=\:\mathrm{0} \\ $$
Commented by mohammad17 last updated on 05/Mar/21

$${sir}\:{why}\:\left({x}+{ix}^{\mathrm{2}} \right){replace}\:{z}\:{in}\:\left({a}\right) \\ $$
Commented by Olaf last updated on 05/Mar/21
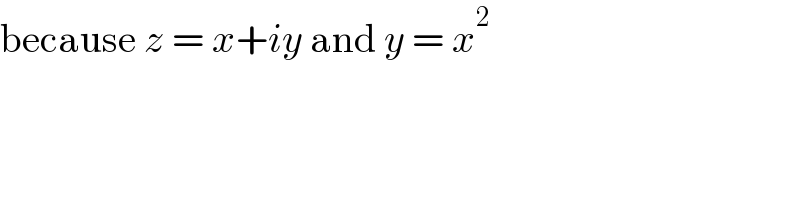
$$\mathrm{because}\:{z}\:=\:{x}+{iy}\:\mathrm{and}\:{y}\:=\:{x}^{\mathrm{2}} \\ $$
Commented by mohammad17 last updated on 05/Mar/21

$${yes}\:{yes}\:{sir}\:{thank}\:{you}\: \\ $$
