Question Number 167305 by greogoury55 last updated on 12/Mar/22
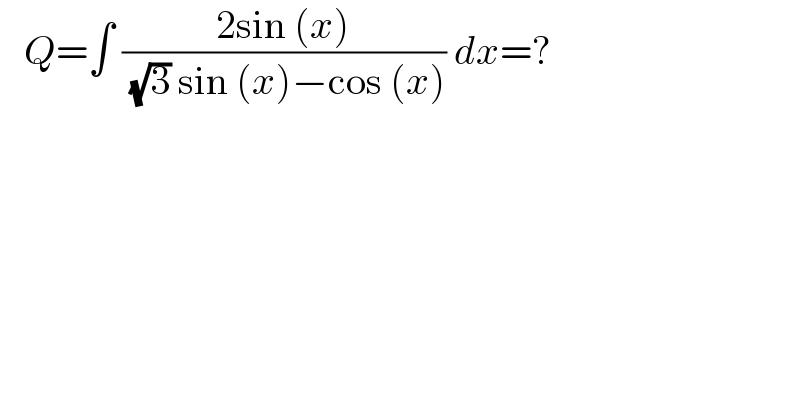
$$\:\:\:{Q}=\int\:\frac{\mathrm{2sin}\:\left({x}\right)}{\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:\left({x}\right)−\mathrm{cos}\:\left({x}\right)}\:{dx}=? \\ $$
Answered by amin96 last updated on 13/Mar/22
![Q=∫((sin(x))/(((√3)/2)sin(x)−(1/2)cos(x)))dx= =−∫((sin(x))/(sin((π/6)−x)))dx (π/6)−x =t x=(π/6)−t Q=∫((sin((π/6)−t))/(sin(t)))dt= =−∫((sin(t−(π/6)))/(sin(t)))=−(1/2)∫(((√3)sin(t)−cos(t))/(sin(t)))dt= =−(1/2)(∫(√3)tdt−∫ctg(t)dt)= =−(1/2)[t(√3)−ln(sin(sin(t))]_(t=(π/6)−x) +c= =−(1/2)(((π(√3))/6)−x(√3)−ln(sin((π/6)−x))+c= =−((π(√3))/(12))+((x(√3))/2)+((ln(sin((π/6)−x)))/2)+c= =(1/2)(x(√3)+ln(sin((π/6)−x))+c](https://www.tinkutara.com/question/Q167327.png)
$${Q}=\int\frac{{sin}\left({x}\right)}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sin}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{cos}\left({x}\right)}{dx}= \\ $$$$=−\int\frac{{sin}\left({x}\right)}{{sin}\left(\frac{\pi}{\mathrm{6}}−{x}\right)}{dx}\:\:\:\:\:\:\:\:\frac{\pi}{\mathrm{6}}−{x}\:={t} \\ $$$${x}=\frac{\pi}{\mathrm{6}}−{t}\:\:\:\:\:{Q}=\int\frac{{sin}\left(\frac{\pi}{\mathrm{6}}−{t}\right)}{{sin}\left({t}\right)}{dt}= \\ $$$$=−\int\frac{{sin}\left({t}−\frac{\pi}{\mathrm{6}}\right)}{{sin}\left({t}\right)}=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\mathrm{3}}{sin}\left({t}\right)−{cos}\left({t}\right)}{{sin}\left({t}\right)}{dt}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\int\sqrt{\mathrm{3}}{tdt}−\int{ctg}\left({t}\right){dt}\right)= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[{t}\sqrt{\mathrm{3}}−{ln}\left({sin}\left({sin}\left({t}\right)\right)\right]_{{t}=\frac{\pi}{\mathrm{6}}−{x}} +{c}=\right. \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}}−{x}\sqrt{\mathrm{3}}−{ln}\left({sin}\left(\frac{\pi}{\mathrm{6}}−{x}\right)\right)+{c}=\right. \\ $$$$=−\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{12}}+\frac{{x}\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{{ln}\left({sin}\left(\frac{\pi}{\mathrm{6}}−{x}\right)\right)}{\mathrm{2}}+{c}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}\sqrt{\mathrm{3}}+{ln}\left({sin}\left(\frac{\pi}{\mathrm{6}}−{x}\right)\right)+{c}\:\:\:\right. \\ $$
