Question Number 101783 by I want to learn more last updated on 04/Jul/20
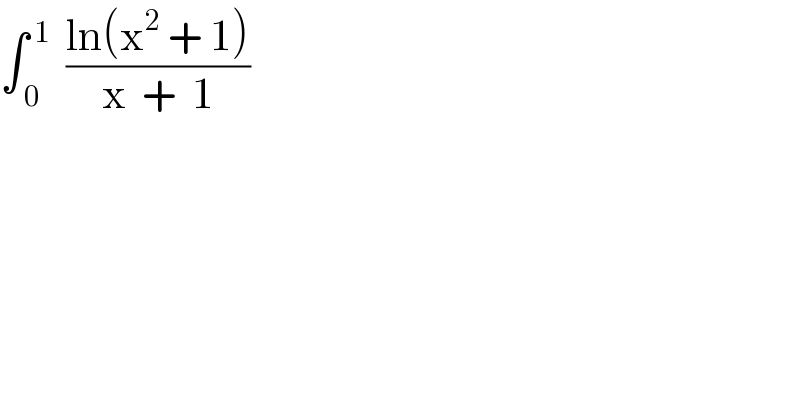
$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\:\frac{\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}{\mathrm{x}\:\:+\:\:\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 04/Jul/20
![let f(a) =∫_0 ^1 ((ln(1+ax^2 ))/(x+1)) with a>0 f^′ (a) =∫_0 ^1 (x^2 /((1+ax^2 )(x+1))) =(1/a)∫_0 ^1 ((1+ax^2 −1)/((1+ax^2 )(x+1)))dx =(1/a)∫_0 ^1 (dx/(x+1)) −(1/a)∫_0 ^1 (dx/((1+ax^2 )(x+1))) ((√a)x =u) =(1/a)[ln∣x+1∣]_0 ^1 −(1/(a(√a))) ∫_0 ^(√a) (du/((1+u^2 )((u/( (√a))) +1))) =(1/a)ln(2)−(1/a) ∫_0 ^(√a) (du/((u^2 +1)(u+(√a)))) let decompose F(u) =(1/((u^2 +1)(u+(√a)))) F(u) =((αu+β)/(u^2 +1)) +(c/(u+(√a))) c =(1/(a+1)) ,lim_(u→+∞) uF(u) =0 =α +c ⇒α =−(1/(a+1)) ⇒F(o) =(1/( (√a))) =β +(c/( (√a))) ⇒β =(1/( (√a)))−(c/( (√a))) =(1/( (√a)))(1−(1/(a+1))) =(a/( (√a)(a+1))) =((√a)/(a+1)) ⇒F(u) =((−(u/(a+1))+(1/(a+1)))/(u^2 +1)) +(1/((a+1)(u+(√a)))) ⇒ ∫_0 ^(√a) F(u)du =−(1/(a+1)) ∫_0 ^(√a) ((u−1)/(u^2 +1))du +(1/(a+1))∫_0 ^(√a) (du/(u+(√a))) =−(1/(2(a+1)))[ln(1+u^2 )]_0 ^(√a) +(1/(a+1))[arctanu]_0 ^(√a) −(1/(a+1))[ln(u+(√a))]_0 ^(√a) =−(1/(2(a+1)))ln(1+a)+(1/(a+1))arctan((√a))−(1/(a+1)){ln(2(√a))−ln((√a))} ⇒ f(a)=((ln(2))/a) −(1/2) ∫ ((ln(1+a))/(a(a+1)))da−∫ ((arctan((√a)))/(a(a+1)))da −ln(2)∫ (da/(a(a+1))) +c be continued....](https://www.tinkutara.com/question/Q101818.png)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{ax}^{\mathrm{2}} \right)}{\mathrm{x}+\mathrm{1}}\:\:\mathrm{with}\:\mathrm{a}>\mathrm{0} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{ax}^{\mathrm{2}} \right)\left(\mathrm{x}+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+\mathrm{ax}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}+\mathrm{ax}^{\mathrm{2}} \right)\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+{ax}^{\mathrm{2}} \right)\left({x}+\mathrm{1}\right)}\:\:\left(\sqrt{{a}}{x}\:={u}\right) \\ $$$$=\frac{\mathrm{1}}{{a}}\left[{ln}\mid\mathrm{x}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{\mathrm{1}}{\mathrm{a}\sqrt{\mathrm{a}}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:\:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\frac{\mathrm{u}}{\:\sqrt{\mathrm{a}}}\:+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:\:\frac{\mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{u}+\sqrt{\mathrm{a}}\right)}\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{u}+\sqrt{\mathrm{a}}\right)} \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\alpha\mathrm{u}+\beta}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{c}}{\mathrm{u}+\sqrt{\mathrm{a}}} \\ $$$$\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\:\:\:,\mathrm{lim}_{\mathrm{u}\rightarrow+\infty} \mathrm{uF}\left(\mathrm{u}\right)\:=\mathrm{0}\:=\alpha\:+\mathrm{c}\:\Rightarrow\alpha\:=−\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{o}\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\:=\beta\:+\frac{\mathrm{c}}{\:\sqrt{\mathrm{a}}}\:\Rightarrow\beta\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}−\frac{\mathrm{c}}{\:\sqrt{\mathrm{a}}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\right)\:=\frac{\mathrm{a}}{\:\sqrt{\mathrm{a}}\left(\mathrm{a}+\mathrm{1}\right)}\:=\frac{\sqrt{\mathrm{a}}}{\mathrm{a}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{u}\right)\:=\frac{−\frac{\mathrm{u}}{\mathrm{a}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{1}}{\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{u}+\sqrt{\mathrm{a}}\right)}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:\mathrm{F}\left(\mathrm{u}\right)\mathrm{du}\:=−\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:\frac{\mathrm{u}−\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du}\:+\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:\:\frac{\mathrm{du}}{\mathrm{u}+\sqrt{\mathrm{a}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{a}+\mathrm{1}\right)}\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:+\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\left[\mathrm{arctanu}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:−\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\left[\mathrm{ln}\left(\mathrm{u}+\sqrt{\mathrm{a}}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{a}+\mathrm{1}\right)}\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)+\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\mathrm{arctan}\left(\sqrt{\mathrm{a}}\right)−\frac{\mathrm{1}}{\mathrm{a}+\mathrm{1}}\left\{\mathrm{ln}\left(\mathrm{2}\sqrt{\mathrm{a}}\right)−\mathrm{ln}\left(\sqrt{\mathrm{a}}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{a}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)}{\mathrm{a}\left(\mathrm{a}+\mathrm{1}\right)}\mathrm{da}−\int\:\frac{\mathrm{arctan}\left(\sqrt{\mathrm{a}}\right)}{\mathrm{a}\left(\mathrm{a}+\mathrm{1}\right)}\mathrm{da}\:−\mathrm{ln}\left(\mathrm{2}\right)\int\:\:\frac{\mathrm{da}}{\mathrm{a}\left(\mathrm{a}+\mathrm{1}\right)}\:+\mathrm{c} \\ $$$$\mathrm{be}\:\mathrm{continued}…. \\ $$
Commented by I want to learn more last updated on 05/Jul/20

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{with}\:\mathrm{just}\:\mathrm{one}\:\mathrm{thing}.. \\ $$$$\mathrm{What}\:\mathrm{type}\:\mathrm{of}\:\mathrm{integration}\:\mathrm{is}\:\mathrm{this},\:\mathrm{what}\:\mathrm{topic}\:\mathrm{exactly} \\ $$$$\mathrm{can}\:\mathrm{i}\:\mathrm{learn}\:\mathrm{integrals}\:\mathrm{like}\:\mathrm{this}. \\ $$
Commented by mathmax by abdo last updated on 05/Jul/20

$$\mathrm{its}\:\mathrm{a}\:\mathrm{paremetric}\:\mathrm{integration}… \\ $$
Commented by mathmax by abdo last updated on 05/Jul/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{giving}\:\mathrm{this}\:\mathrm{explanation}… \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jul/20
![If the question is ∫_0 ^1 ((log(x+1))/(x^2 +1)) Then ∫_0 ^1 ((log(tanθ+1))/(sec^2 θ))sec^2 θdθ { suppose x=tanθ ∫_0 ^(π/4) log(sinθ+cosθ)−log(cosθ)dθ ∫_0 ^(π/4) log((√2)(cos((π/4)−θ)))−log(cosθ) ∫_0 ^(π/4) log(√2)+log(cos((π/4)−θ))−log(cosθ)=I {∫_0 ^(π/4) f(θ)=∫_0 ^(π/4) f((π/4)−θ) ∫_0 ^(π/4) log(√2)+log(cos(θ))−log(cos((π/4)−θ)=I {adding } 2I=2∫_0 ^(π/4) log(√2)dθ I=(1/2)log2[θ]_0 ^(π/4) I=(π/8)log2](https://www.tinkutara.com/question/Q101875.png)
$${If}\:{the}\:{question}\:{is}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${Then}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({tan}\theta+\mathrm{1}\right)}{{sec}^{\mathrm{2}} \theta}{sec}^{\mathrm{2}} \theta{d}\theta\:\:\:\:\left\{\:\:{suppose}\:{x}={tan}\theta\right. \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({sin}\theta+{cos}\theta\right)−{log}\left({cos}\theta\right){d}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left(\sqrt{\mathrm{2}}\left({cos}\left(\frac{\pi}{\mathrm{4}}−\theta\right)\right)\right)−{log}\left({cos}\theta\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\sqrt{\mathrm{2}}+{log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−\theta\right)\right)−{log}\left({cos}\theta\right)={I}\:\:\:\:\left\{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {f}\left(\theta\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {f}\left(\frac{\pi}{\mathrm{4}}−\theta\right)\right. \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\sqrt{\mathrm{2}}+{log}\left({cos}\left(\theta\right)\right)−{log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−\theta\right)={I}\:\:\:\left\{{adding}\:\right\}\right. \\ $$$$\mathrm{2}{I}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\sqrt{\mathrm{2}}{d}\theta \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{log}\mathrm{2}\left[\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$${I}=\frac{\pi}{\mathrm{8}}{log}\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 05/Jul/20

$$\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{question}…! \\ $$
Commented by Dwaipayan Shikari last updated on 05/Jul/20

$${I}\:{have}\:{edited}\:{it}.{But}\:{sir}\:{you}\:{are}\:{right},{this}\:{is}\:{not}\:{the}\:{question}. \\ $$$${I}\:{am}\:{trying}\:. \\ $$
Commented by 1549442205 last updated on 05/Jul/20
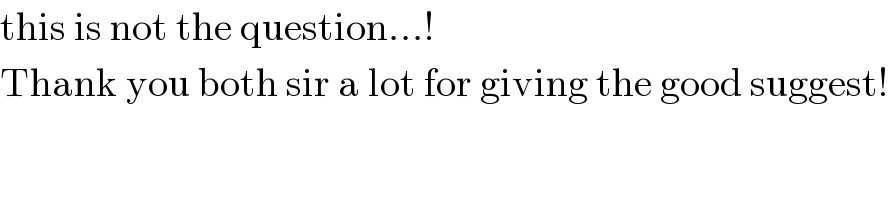
$$\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{question}…! \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{both}\:\mathrm{sir}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{for}\:\mathrm{giving}\:\mathrm{the}\:\mathrm{good}\:\mathrm{suggest}! \\ $$
