Question Number 36314 by behi83417@gmail.com last updated on 31/May/18

Commented by behi83417@gmail.com last updated on 31/May/18
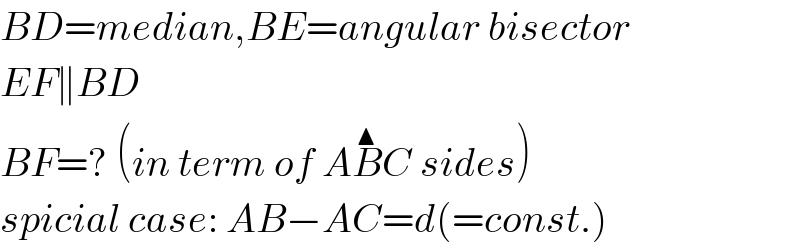
$${BD}={median},{BE}={angular}\:{bisector} \\ $$$${EF}\parallel{BD} \\ $$$${BF}=?\:\left({in}\:{term}\:{of}\:{A}\overset{\blacktriangle} {{B}C}\:{sides}\right) \\ $$$${spicial}\:{case}:\:{AB}−{AC}={d}\left(={const}.\right) \\ $$
Answered by ajfour last updated on 31/May/18
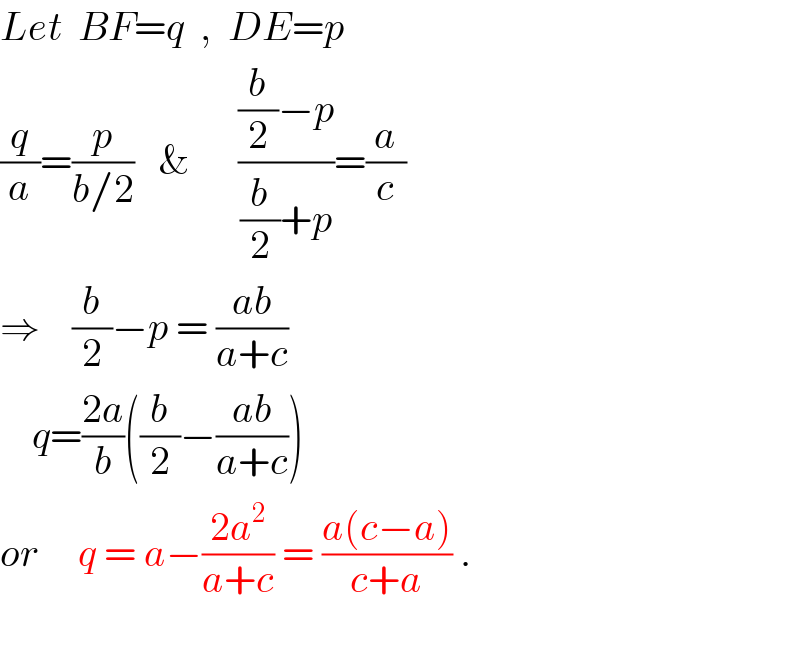
$${Let}\:\:{BF}={q}\:\:,\:\:{DE}={p} \\ $$$$\frac{{q}}{{a}}=\frac{{p}}{{b}/\mathrm{2}}\:\:\:\&\:\:\:\:\:\:\frac{\frac{{b}}{\mathrm{2}}−{p}}{\frac{{b}}{\mathrm{2}}+{p}}=\frac{{a}}{{c}} \\ $$$$\Rightarrow\:\:\:\:\frac{{b}}{\mathrm{2}}−{p}\:=\:\frac{{ab}}{{a}+{c}} \\ $$$$\:\:\:\:{q}=\frac{\mathrm{2}{a}}{{b}}\left(\frac{{b}}{\mathrm{2}}−\frac{{ab}}{{a}+{c}}\right) \\ $$$${or}\:\:\:\:\:{q}\:=\:{a}−\frac{\mathrm{2}{a}^{\mathrm{2}} }{{a}+{c}}\:=\:\frac{{a}\left({c}−{a}\right)}{{c}+{a}}\:. \\ $$$$ \\ $$
Commented by behi83417@gmail.com last updated on 31/May/18
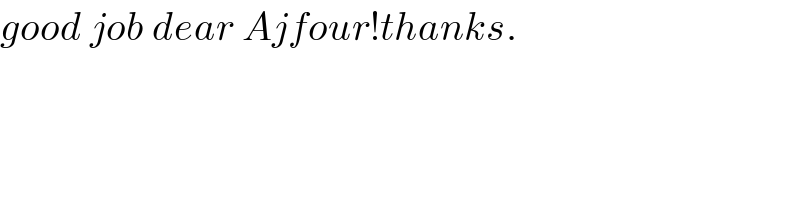
$${good}\:{job}\:{dear}\:{Ajfour}!{thanks}. \\ $$
