if-a-1-4-a-2-1-and-a-n-a-n-1-a-n-3-find-a-4-a-1-

Question Number 101871 by bemath last updated on 05/Jul/20

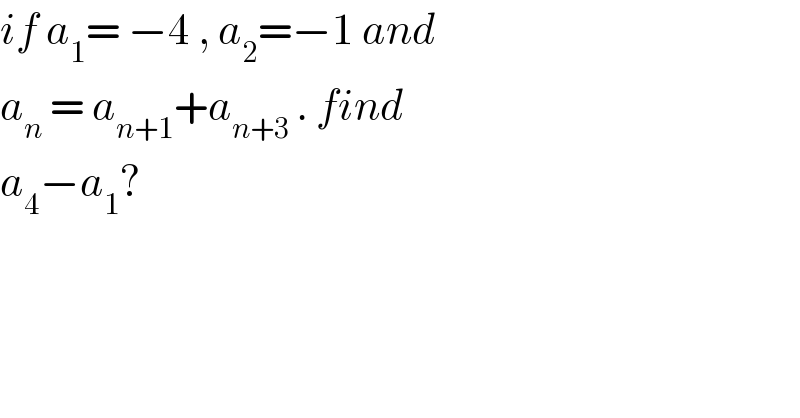
$${if}\:{a}_{\mathrm{1}} =\:−\mathrm{4}\:,\:{a}_{\mathrm{2}} =−\mathrm{1}\:{and}\: \\ $$$${a}_{{n}} \:=\:{a}_{{n}+\mathrm{1}} +{a}_{{n}+\mathrm{3}\:} .\:{find}\: \\ $$$${a}_{\mathrm{4}} −{a}_{\mathrm{1}} ? \\ $$

Answered by Rasheed.Sindhi last updated on 05/Jul/20

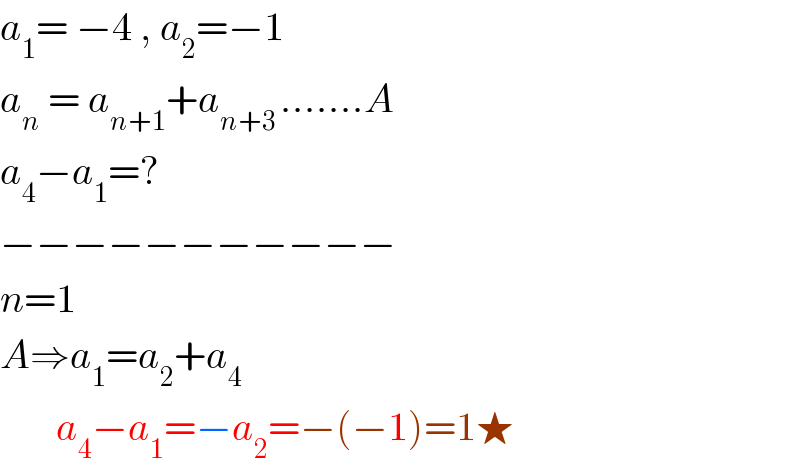
a_1 = −4 , a_2 =−1 a_n = a_(n+1) +a_(n+3 ) .......A a_4 −a_1 =? −−−−−−−−−−− n=1 A⇒a_1 =a_2 +a_4 a_4 −a_1 =−a_2 =−(−1)=1★

$${a}_{\mathrm{1}} =\:−\mathrm{4}\:,\:{a}_{\mathrm{2}} =−\mathrm{1} \\ $$$${a}_{{n}} \:=\:{a}_{{n}+\mathrm{1}} +{a}_{{n}+\mathrm{3}\:} …….{A} \\ $$$${a}_{\mathrm{4}} −{a}_{\mathrm{1}} =? \\ $$$$−−−−−−−−−−− \\ $$$${n}=\mathrm{1} \\ $$$${A}\Rightarrow{a}_{\mathrm{1}} ={a}_{\mathrm{2}} +{a}_{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:{a}_{\mathrm{4}} −{a}_{\mathrm{1}} =−{a}_{\mathrm{2}} =−\left(−\mathrm{1}\right)=\mathrm{1}\bigstar \\ $$

Commented by bemath last updated on 05/Jul/20

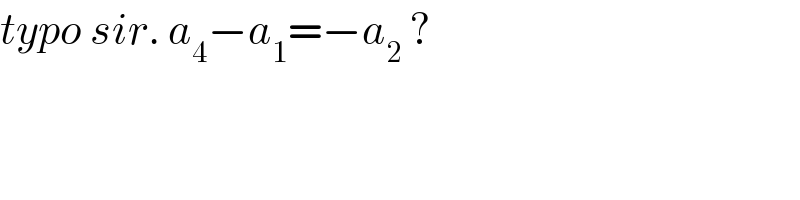
$${typo}\:{sir}.\:{a}_{\mathrm{4}} −{a}_{\mathrm{1}} =−{a}_{\mathrm{2}} \:? \\ $$

Commented by Rasheed.Sindhi last updated on 05/Jul/20

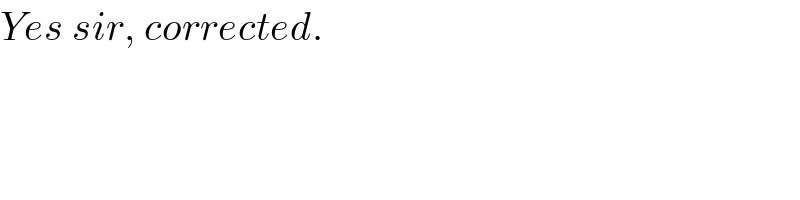
$${Yes}\:{sir},\:{corrected}. \\ $$

Commented by mr W last updated on 05/Jul/20

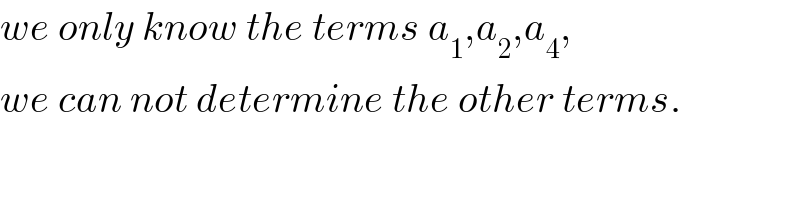
we only know the terms a_1 ,a_2 ,a_4 , we can not determine the other terms.

$${we}\:{only}\:{know}\:{the}\:{terms}\:{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,{a}_{\mathrm{4}} , \\ $$$${we}\:{can}\:{not}\:{determine}\:{the}\:{other}\:{terms}. \\ $$

Facebook Tweet Pin

if-a-1-4-a-2-1-and-a-n-a-n-1-a-n-3-find-a-4-a-1-

Leave a Reply Cancel reply