Question Number 36365 by chakraborty ankit last updated on 01/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 01/Jun/18
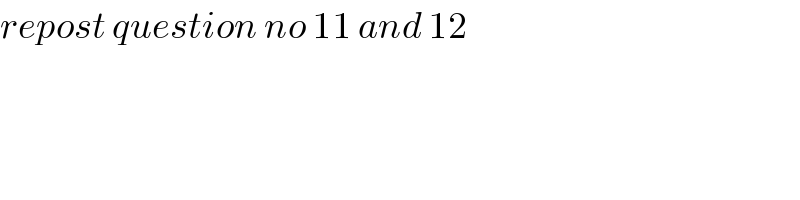
$${repost}\:{question}\:{no}\:\mathrm{11}\:{and}\:\mathrm{12} \\ $$
Commented by chakraborty ankit last updated on 02/Jun/18

$${ok}\:{sir} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jun/18

$$\:\:\:\:\:\:{s}_{{n}} =\mathrm{2}+\mathrm{3}+\mathrm{6}+\mathrm{11}+\mathrm{18}+…+{T}_{{n}−\mathrm{1}} +{T}_{{n}} \\ $$$$\:\:\:\:\:\:\:\:{s}_{{n}} =\:\:\:\:\:\mathrm{2}+\mathrm{3}+\mathrm{6}+\mathrm{11}+…+{T}_{{n}−\mathrm{2}} +{T}_{{n}−\mathrm{1}} +{T}_{{n}} \\ $$$${shifting}\:{one}\:{place}\:{rivhtward}\:{then}\:{subsgructing} \\ $$$$\mathrm{0}=\mathrm{2}+\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+…−{T}_{{n}} \right) \\ $$$${T}_{{n}} =\mathrm{2}+\frac{{n}−\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2}×\mathrm{1}+\left({n}−\mathrm{1}−\mathrm{1}\right)×\mathrm{2}\right\} \\ $$$${T}_{{n}} =\mathrm{2}+\frac{{n}−\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2}{n}−\mathrm{2}\right\} \\ $$$${T}_{{n}} =\mathrm{2}+\left({n}−\mathrm{1}\right)\left({n}−\mathrm{1}\right) \\ $$$${T}_{{n}} ={n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{3} \\ $$$${T}_{\mathrm{50}} =\mathrm{50}^{\mathrm{2}} −\mathrm{2}×\mathrm{50}+\mathrm{3} \\ $$$$=\mathrm{2500}−\mathrm{100}+\mathrm{3} \\ $$$$=\mathrm{2403} \\ $$$$\mathrm{49}^{\mathrm{2}} +\mathrm{2}\:{is}\:{ans} \\ $$$$\: \\ $$$$ \\ $$
