Question Number 36444 by rahul 19 last updated on 02/Jun/18

$$\int\:\frac{\mathrm{d}{x}}{\left(\mathrm{2}{x}−\mathrm{7}\right)\sqrt{\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}}\:=\:? \\ $$
Commented by math1967 last updated on 02/Jun/18
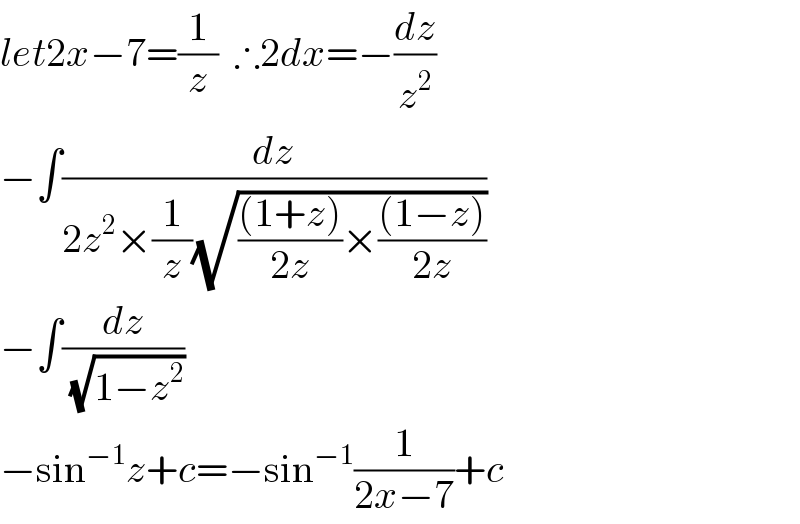
$${let}\mathrm{2}{x}−\mathrm{7}=\frac{\mathrm{1}}{{z}}\:\:\therefore\mathrm{2}{dx}=−\frac{{dz}}{{z}^{\mathrm{2}} } \\ $$$$−\int\frac{{dz}}{\mathrm{2}{z}^{\mathrm{2}} ×\frac{\mathrm{1}}{{z}}\sqrt{\frac{\left(\mathrm{1}+{z}\right)}{\mathrm{2}{z}}×\frac{\left(\mathrm{1}−{z}\right)}{\mathrm{2}{z}}}} \\ $$$$−\int\frac{{dz}}{\:\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }} \\ $$$$−\mathrm{sin}^{−\mathrm{1}} {z}+{c}=−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{7}}+{c} \\ $$
Commented by math1967 last updated on 02/Jun/18

$${Am}\:{I}\:{correct}? \\ $$
Commented by MJS last updated on 02/Jun/18

$$\mathrm{indeed}\:\mathrm{correct}! \\ $$
Commented by rahul 19 last updated on 02/Jun/18

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{confirming}! \\ $$
Commented by MJS last updated on 02/Jun/18
![another way: ∫(dx/((2x−7)(√(x^2 −7x+12))))= [t=(√(x^2 −7x+12)) → dx=((2(√(x^2 −7x+12)))/(2x−7))dt] =2∫(dt/(4t^2 +1))= [u=2t → dt=(du/2)] =∫(du/(u^2 +1))=arctan u=arctan 2t= =arctan 2(√((x−3)(x−4)))+C](https://www.tinkutara.com/question/Q36460.png)
$$\mathrm{another}\:\mathrm{way}: \\ $$$$\int\frac{{dx}}{\left(\mathrm{2}{x}−\mathrm{7}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}}}{\mathrm{2}{x}−\mathrm{7}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{2}{t}\:\rightarrow\:{dt}=\frac{{du}}{\mathrm{2}}\right] \\ $$$$=\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\mathrm{arctan}\:{u}=\mathrm{arctan}\:\mathrm{2}{t}= \\ $$$$=\mathrm{arctan}\:\mathrm{2}\sqrt{\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}+{C} \\ $$
Commented by math1967 last updated on 02/Jun/18

$${It}\:{is}\:{more}\:{easy}.{Thanks}\:{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18

$$\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)={x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}\:\:\:{not}\:{x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{12} \\ $$
Commented by math1967 last updated on 02/Jun/18

$${you}\:{are}\:{correct}\:{Tanmay}\:{sir} \\ $$
Commented by MJS last updated on 02/Jun/18

$$\mathrm{sorry},\:\mathrm{typo}.\:\mathrm{I}\:\mathrm{corrected}\:\mathrm{it} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18

Commented by prof Abdo imad last updated on 03/Jun/18

$${changement}\:\:\mathrm{2}{x}−\mathrm{7}={t}\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\:\:\frac{\mathrm{1}}{{t}\sqrt{\left(\frac{{t}+\mathrm{7}}{\mathrm{2}}−\mathrm{3}\right)\left(\frac{{t}+\mathrm{7}}{\mathrm{2}}\:−\mathrm{4}\right)}}\frac{{dt}}{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{\mathrm{2}{dt}}{{t}\sqrt{\left({t}+\mathrm{1}\right)\left({t}−\mathrm{1}\right)}} \\ $$$$=\:\int\:\:\:\:\:\frac{{dt}}{{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\:{and}\:{changement}\:{t}\:={ch}\left({u}\right)\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\:\frac{{sh}\left({u}\right)}{{ch}\left({u}\right){shu}}{du}\:=\:\int\:\:\:\:\:\frac{{du}}{{chu}} \\ $$$$=\int\:\:\:\:\frac{\mathrm{2}{du}}{{e}^{{u}} \:+{e}^{−{u}} }\:=_{{e}^{{u}} ={x}} \:\:\int\:\:\:\:\:\frac{\mathrm{2}}{{x}\:+\frac{\mathrm{1}}{{x}}}\:\frac{{dx}}{{x}} \\ $$$$=\:\mathrm{2}\:\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{2}{arctanx}\:+{c} \\ $$$$=\mathrm{2}{arctan}\left(\:{e}^{{u}} \right)\:=\:\mathrm{2}{arctan}\:\left(\:{e}^{{argch}\left({t}\right)} \right)\:+{c} \\ $$$$=\:\mathrm{2}{arctan}\:\left({ln}\left({t}\:+\sqrt{\left.{t}^{\mathrm{2}} −\mathrm{1}\right)}\:\:+{c}\right.\right. \\ $$$$=\mathrm{2}{arctan}\left\{{ln}\left(\mathrm{2}{x}−\mathrm{7}\:+\sqrt{\left.\left(\mathrm{2}{x}−\mathrm{7}\right)^{\mathrm{2}} \:−\mathrm{1}\right)}\right\}\:+{c}\:.\right. \\ $$$$ \\ $$
