Question Number 102058 by Dwaipayan Shikari last updated on 06/Jul/20
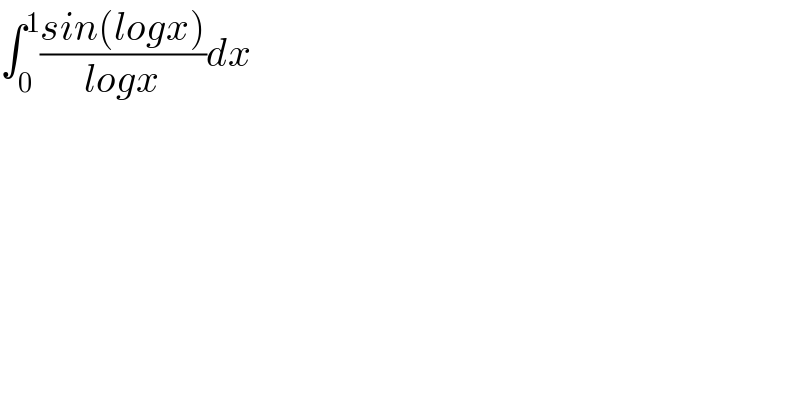
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left({logx}\right)}{{logx}}{dx} \\ $$
Answered by prakash jain last updated on 06/Jul/20
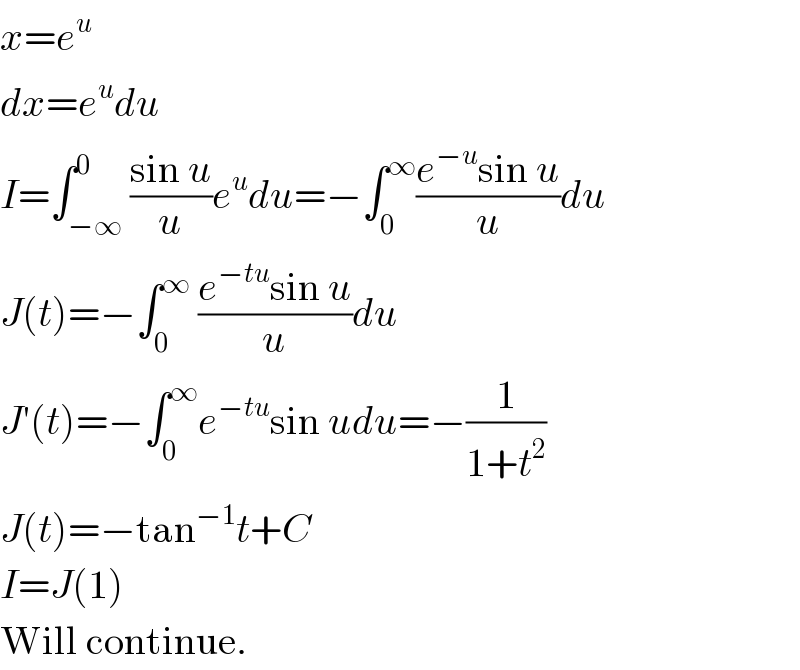
$${x}={e}^{{u}} \\ $$$${dx}={e}^{{u}} {du} \\ $$$${I}=\int_{−\infty} ^{\mathrm{0}} \frac{\mathrm{sin}\:{u}}{{u}}{e}^{{u}} {du}=−\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{u}} \mathrm{sin}\:{u}}{{u}}{du} \\ $$$${J}\left({t}\right)=−\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{tu}} \mathrm{sin}\:{u}}{{u}}{du} \\ $$$${J}'\left({t}\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−{tu}} \mathrm{sin}\:{udu}=−\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${J}\left({t}\right)=−\mathrm{tan}^{−\mathrm{1}} {t}+{C} \\ $$$${I}={J}\left(\mathrm{1}\right) \\ $$$$\mathrm{Will}\:\mathrm{continue}. \\ $$
