Question Number 102065 by bramlex last updated on 06/Jul/20
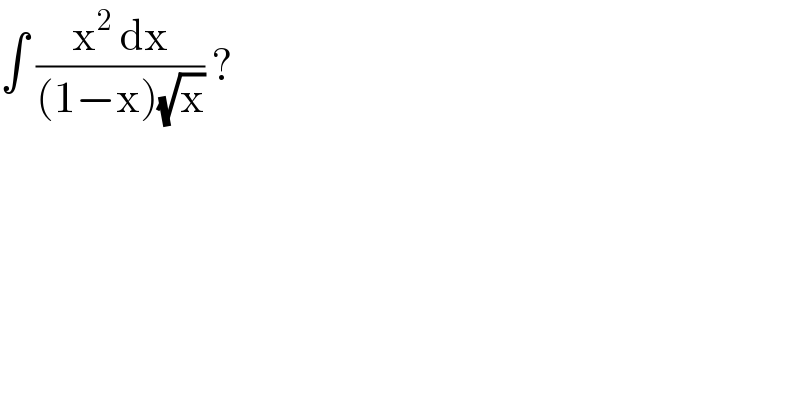
$$\int\:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{dx}}{\left(\mathrm{1}−\mathrm{x}\right)\sqrt{\mathrm{x}}}\:? \\ $$
Answered by PRITHWISH SEN 2 last updated on 06/Jul/20

$$\int\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}−\mathrm{x}\right)\sqrt{\mathrm{x}}}\:\mathrm{dx}=\int\frac{\mathrm{dx}}{\left(\mathrm{1}−\mathrm{x}\right)\sqrt{\mathrm{x}}}\:−\int\frac{\left(\mathrm{1}+\mathrm{x}\right)}{\:\sqrt{\mathrm{x}}}\mathrm{dx} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{part}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{part} \\ $$$$\sqrt{\mathrm{x}}=\mathrm{t}\Rightarrow\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}}}\:=\:\mathrm{2dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{x}}=\mathrm{u}\Rightarrow\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}}}\:=\mathrm{2du} \\ $$$$=\int\frac{\mathrm{2dt}}{\mathrm{t}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}−\mathrm{2}\int\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\mathrm{du} \\ $$$$=\mathrm{2}\int\frac{\mathrm{dt}}{\mathrm{t}}+\int\frac{\mathrm{2tdt}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:−\mathrm{2u}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{u}^{\mathrm{3}} \:+\mathrm{c}_{\mathrm{1}} \\ $$$$=\mathrm{ln}\left(\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}}\right)−\mathrm{2}\sqrt{\mathrm{x}}\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}\sqrt{\mathrm{x}}\:+\mathrm{c} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$
