Question Number 167648 by mathlove last updated on 22/Mar/22
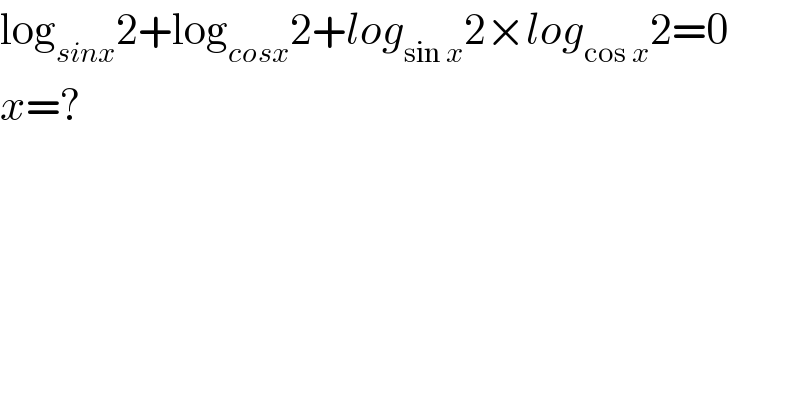
$$\mathrm{log}_{{sinx}} \mathrm{2}+\mathrm{log}_{{cosx}} \mathrm{2}+{log}_{\mathrm{sin}\:{x}} \mathrm{2}×{log}_{\mathrm{cos}\:{x}} \mathrm{2}=\mathrm{0} \\ $$$${x}=? \\ $$
Commented by Rasheed.Sindhi last updated on 22/Mar/22
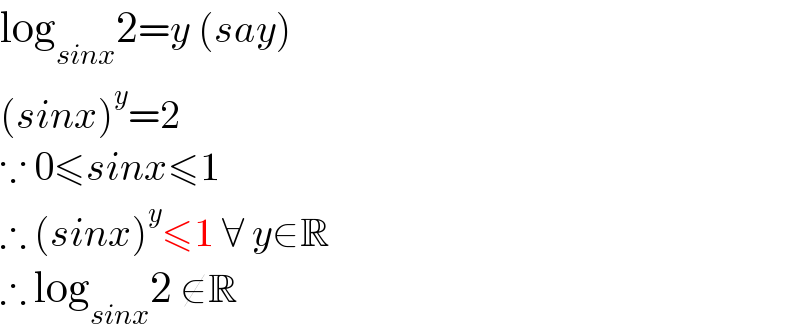
$$\mathrm{log}_{{sinx}} \mathrm{2}={y}\:\left({say}\right) \\ $$$$\left({sinx}\right)^{{y}} =\mathrm{2} \\ $$$$\because\:\mathrm{0}\leqslant{sinx}\leqslant\mathrm{1} \\ $$$$\therefore\:\left({sinx}\right)^{{y}} \leqslant\mathrm{1}\:\forall\:{y}\in\mathbb{R} \\ $$$$\therefore\:\mathrm{log}_{{sinx}} \mathrm{2}\:\notin\mathbb{R} \\ $$
Commented by Nimatullah last updated on 22/Mar/22
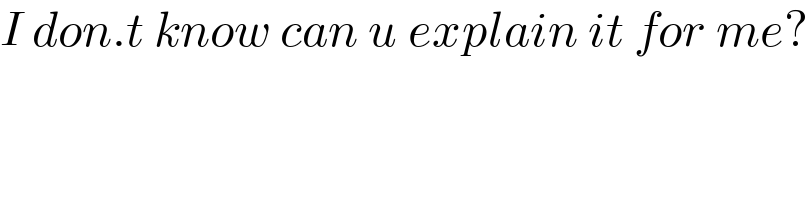
$${I}\:{don}.{t}\:{know}\:{can}\:{u}\:{explain}\:{it}\:{for}\:{me}? \\ $$
Commented by Nimatullah last updated on 22/Mar/22

$${plz}\:{ans} \\ $$
Commented by Rasheed.Sindhi last updated on 22/Mar/22

$${Which}\:{step}\:{do}\:{you}\:{not}\:{understand}? \\ $$
Commented by Nimatullah last updated on 22/Mar/22
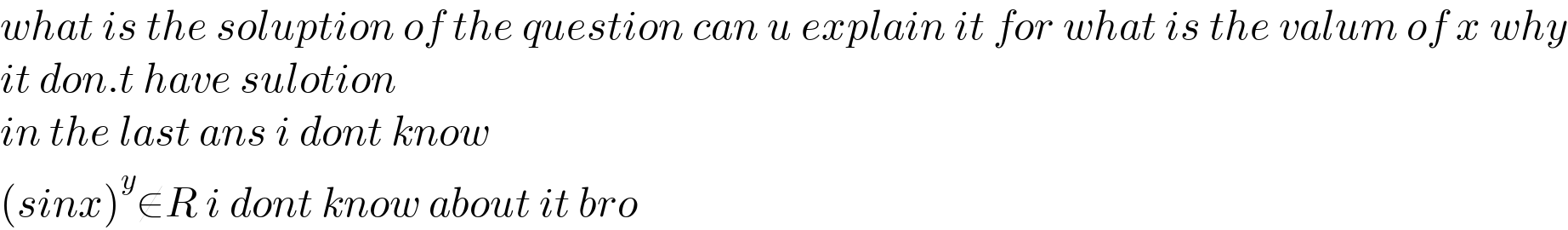
$${what}\:{is}\:{the}\:{soluption}\:{of}\:{the}\:{question}\:{can}\:{u}\:{explain}\:{it}\:{for}\:{what}\:{is}\:{the}\:{valum}\:{of}\:{x}\:{why} \\ $$$${it}\:{don}.{t}\:{have}\:{sulotion}\: \\ $$$${in}\:{the}\:{last}\:{ans}\:{i}\:{dont}\:{know} \\ $$$$\left({sinx}\right)^{{y}} \notin{R}\:{i}\:{dont}\:{know}\:{about}\:{it}\:{bro} \\ $$
Commented by Rasheed.Sindhi last updated on 22/Mar/22

$${I}\:{think}\:{I}'{m}\:{wrong}.\:{For}\:{negative}\:{y} \\ $$$$\left({sinx}\right)^{{y}} \:{may}\:{be}\:{greater}\:{than}\:\mathrm{1}. \\ $$$${Thank}\:{you}\:{Nimatullah}\:{to}\:{point}\:{out} \\ $$$${my}\:{mistake}. \\ $$
