Menu Close

B-1-sin-6x-1-sin-6x-dx-

Tinku Tara 0 Comments
Pin




Question Number 134641 by benjo_mathlover last updated on 06/Mar/21
B = ∫ ((1−sin 6x)/(1+sin 6x)) dx
$$\mathscr{B}\:=\:\int\:\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{6}{x}}{\mathrm{1}+\mathrm{sin}\:\mathrm{6}{x}}\:{dx}\: \\ $$
Answered by Dwaipayan Shikari last updated on 06/Mar/21
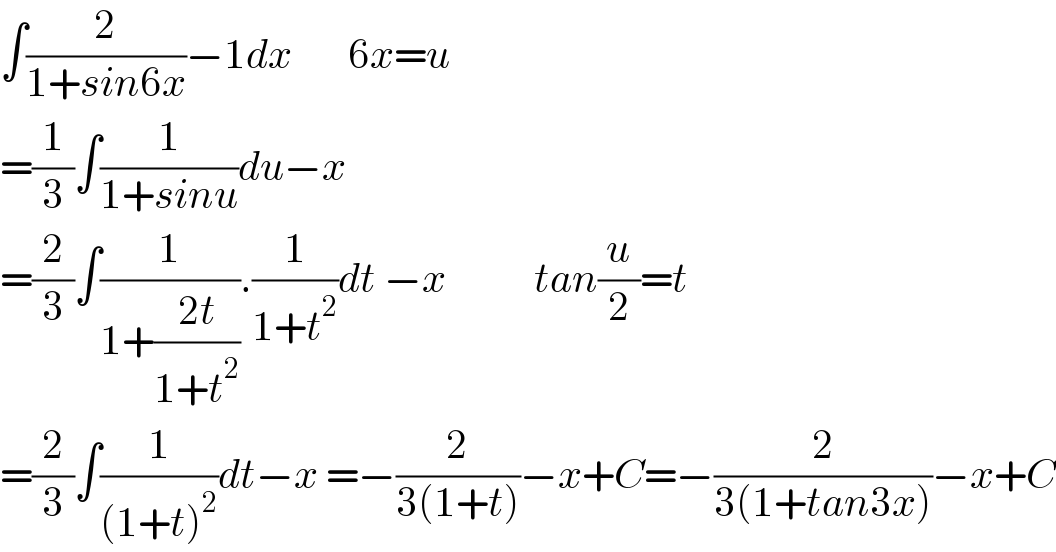
∫(2/(1+sin6x))−1dx 6x=u =(1/3)∫(1/(1+sinu))du−x =(2/3)∫(1/(1+((2t)/(1+t^2 )))).(1/(1+t^2 ))dt −x tan(u/2)=t =(2/3)∫(1/((1+t)^2 ))dt−x =−(2/(3(1+t)))−x+C=−(2/(3(1+tan3x)))−x+C
$$\int\frac{\mathrm{2}}{\mathrm{1}+{sin}\mathrm{6}{x}}−\mathrm{1}{dx}\:\:\:\:\:\:\:\mathrm{6}{x}={u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{\mathrm{1}+{sinu}}{du}−{x}\:\: \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:−{x}\:\:\:\:\:\:\:\:\:\:\:{tan}\frac{{u}}{\mathrm{2}}={t} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}−{x}\:=−\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{1}+{t}\right)}−{x}+{C}=−\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{1}+{tan}\mathrm{3}{x}\right)}−{x}+{C} \\ $$
Answered by Olaf last updated on 06/Mar/21
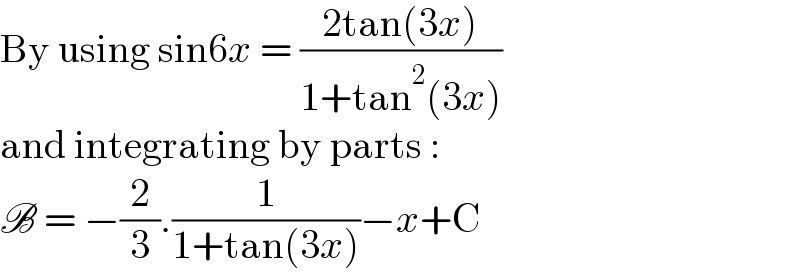
By using sin6x = ((2tan(3x))/(1+tan^2 (3x))) and integrating by parts : B = −(2/3).(1/(1+tan(3x)))−x+C
$$\mathrm{By}\:\mathrm{using}\:\mathrm{sin6}{x}\:=\:\frac{\mathrm{2tan}\left(\mathrm{3}{x}\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{3}{x}\right)} \\ $$$$\mathrm{and}\:\mathrm{integrating}\:\mathrm{by}\:\mathrm{parts}\:: \\ $$$$\mathscr{B}\:=\:−\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}\left(\mathrm{3}{x}\right)}−{x}+\mathrm{C} \\ $$
Answered by EDWIN88 last updated on 06/Mar/21
B =∫ ((1−sin 6x)/(1+sin 6x)) dx = ∫ tan^2 ((π/4)−3x)dx B = ∫ [sec^2 ((π/4)−3x)−1] dx B = −(1/3)tan ((π/4)−3x)−x + c
$$\mathscr{B}\:=\int\:\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{6x}}{\mathrm{1}+\mathrm{sin}\:\mathrm{6x}}\:\mathrm{dx}\:=\:\int\:\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\mathrm{3x}\right)\mathrm{dx} \\ $$$$\mathscr{B}\:=\:\int\:\left[\mathrm{sec}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\mathrm{3x}\right)−\mathrm{1}\right]\:\mathrm{dx} \\ $$$$\mathscr{B}\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\mathrm{3x}\right)−\mathrm{x}\:+\:\mathrm{c}\: \\ $$
Answered by Ar Brandon last updated on 06/Mar/21
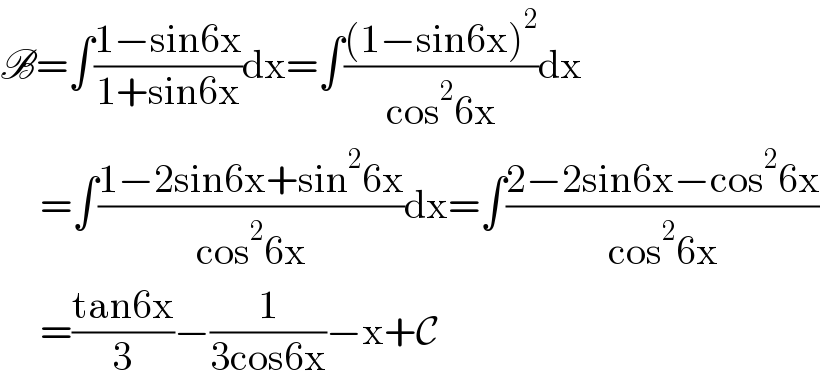
B=∫((1−sin6x)/(1+sin6x))dx=∫(((1−sin6x)^2 )/(cos^2 6x))dx =∫((1−2sin6x+sin^2 6x)/(cos^2 6x))dx=∫((2−2sin6x−cos^2 6x)/(cos^2 6x)) =((tan6x)/3)−(1/(3cos6x))−x+C
$$\mathscr{B}=\int\frac{\mathrm{1}−\mathrm{sin6x}}{\mathrm{1}+\mathrm{sin6x}}\mathrm{dx}=\int\frac{\left(\mathrm{1}−\mathrm{sin6x}\right)^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \mathrm{6x}}\mathrm{dx} \\ $$$$\:\:\:\:\:=\int\frac{\mathrm{1}−\mathrm{2sin6x}+\mathrm{sin}^{\mathrm{2}} \mathrm{6x}}{\mathrm{cos}^{\mathrm{2}} \mathrm{6x}}\mathrm{dx}=\int\frac{\mathrm{2}−\mathrm{2sin6x}−\mathrm{cos}^{\mathrm{2}} \mathrm{6x}}{\mathrm{cos}^{\mathrm{2}} \mathrm{6x}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{tan6x}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3cos6x}}−\mathrm{x}+\mathcal{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *