Question-36700

Question Number 36700 by rahul 19 last updated on 04/Jun/18

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jun/18

R_2 andR_x parralal so equivalant resistance =((30x)/(30+x)) total resistance=R=20+((30x)/(30+x)) =((600+50x)/(30+x)) thermal power=(V^2 /R) p=((V^2 ×(30+x))/(600+50x)) now xchanges to x+△x p changes to p+△p to show when △x→0 △p→0 p+△p=V^2 ×(((30+x+△x))/(600+50x+50△x)) △p=V^2 ×{((30+x+△x)/(600+50x+50△x))−((30+x)/(600+50x))} =V^2 {((18000+1500x+600x+50x^2 +△x(600+50x))/) ((−18000−1500x−1500△x−600x−50x^2 −x50△x)/) =(N_r /D_r ) when △x→0 the value of N_r →0 that means △p→0 hence proved

$${R}_{\mathrm{2}} {andR}_{{x}} \:{parralal}\:{so}\:{equivalant}\:{resistance} \\ $$$$=\frac{\mathrm{30}{x}}{\mathrm{30}+{x}} \\ $$$${total}\:{resistance}={R}=\mathrm{20}+\frac{\mathrm{30}{x}}{\mathrm{30}+{x}} \\ $$$$=\frac{\mathrm{600}+\mathrm{50}{x}}{\mathrm{30}+{x}} \\ $$$${thermal}\:{power}=\frac{{V}^{\mathrm{2}} }{{R}} \\ $$$${p}=\frac{{V}^{\mathrm{2}} ×\left(\mathrm{30}+{x}\right)}{\mathrm{600}+\mathrm{50}{x}} \\ $$$${now}\:{xchanges}\:{to}\:{x}+\bigtriangleup{x} \\ $$$${p}\:{changes}\:{to}\:{p}+\bigtriangleup{p} \\ $$$${to}\:{show}\:{when}\:\bigtriangleup{x}\rightarrow\mathrm{0} \\ $$$$\bigtriangleup{p}\rightarrow\mathrm{0} \\ $$$${p}+\bigtriangleup{p}={V}^{\mathrm{2}} ×\frac{\left(\mathrm{30}+{x}+\bigtriangleup{x}\right)}{\mathrm{600}+\mathrm{50}{x}+\mathrm{50}\bigtriangleup{x}} \\ $$$$\bigtriangleup{p}={V}^{\mathrm{2}} ×\left\{\frac{\mathrm{30}+{x}+\bigtriangleup{x}}{\mathrm{600}+\mathrm{50}{x}+\mathrm{50}\bigtriangleup{x}}−\frac{\mathrm{30}+{x}}{\mathrm{600}+\mathrm{50}{x}}\right\} \\ $$$$={V}^{\mathrm{2}} \left\{\frac{\mathrm{18000}+\mathrm{1500}{x}+\mathrm{600}{x}+\mathrm{50}{x}^{\mathrm{2}} +\bigtriangleup{x}\left(\mathrm{600}+\mathrm{50}{x}\right)}{}\right. \\ $$$$\:\frac{−\mathrm{18000}−\mathrm{1500}{x}−\mathrm{1500}\bigtriangleup{x}−\mathrm{600}{x}−\mathrm{50}{x}^{\mathrm{2}} −{x}\mathrm{50}\bigtriangleup{x}}{} \\ $$$$=\frac{{N}_{{r}} }{{D}_{{r}} } \\ $$$${when}\:\bigtriangleup{x}\rightarrow\mathrm{0}\:\:{the}\:{value}\:{of}\:{N}_{{r}} \rightarrow\mathrm{0} \\ $$$${that}\:{means}\:\bigtriangleup{p}\rightarrow\mathrm{0} \\ $$$${hence}\:{proved} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by rahul 19 last updated on 04/Jun/18

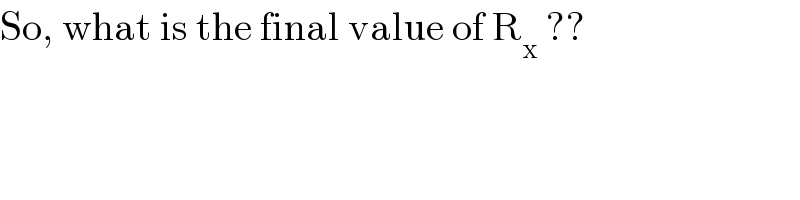
$$\mathrm{So},\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{final}\:\mathrm{value}\:\mathrm{of}\:\mathrm{R}_{\mathrm{x}} \:?? \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 04/Jun/18

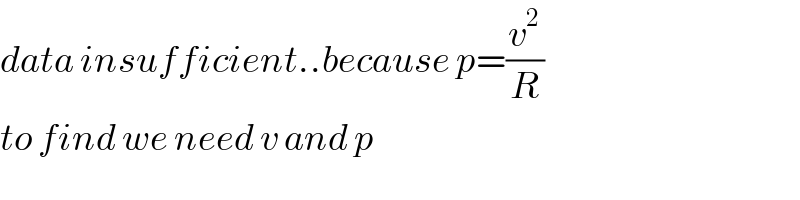
data insufficient..because p=(v^2 /R) to find we need v and p

$${data}\:{insufficient}..{because}\:{p}=\frac{{v}^{\mathrm{2}} }{{R}} \\ $$$${to}\:{find}\:{we}\:{need}\:{v}\:{and}\:{p} \\ $$

Answered by ajfour last updated on 15/Jun/18

let R_x =x P_x =i_x ^2 x P_x = [(V^( 2) /((20+((30x)/(30+x)))^2 ))×(((30)/(30+x)))^2 ]x =((900V^( 2) x)/((1800+50x)^2 )) = ((9V^( 2) )/(25))×(x/((x+36)^2 )) for small variations in x if power doesn′t change much then for such a value of x (dP_x /dx)=0 ; ⇒ (x+36)^2 =2x(x+36) ⇒ x = 18 Ω .

$${let}\:{R}_{{x}} ={x} \\ $$$${P}_{{x}} ={i}_{{x}} ^{\mathrm{2}} {x} \\ $$$${P}_{{x}} =\:\left[\frac{{V}^{\:\:\mathrm{2}} }{\left(\mathrm{20}+\frac{\mathrm{30}{x}}{\mathrm{30}+{x}}\right)^{\mathrm{2}} }×\left(\frac{\mathrm{30}}{\mathrm{30}+{x}}\right)^{\mathrm{2}} \right]{x} \\ $$$$\:\:\:=\frac{\mathrm{900}{V}^{\:\:\mathrm{2}} {x}}{\left(\mathrm{1800}+\mathrm{50}{x}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{9}{V}^{\:\:\mathrm{2}} }{\mathrm{25}}×\frac{{x}}{\left({x}+\mathrm{36}\right)^{\mathrm{2}} } \\ $$$${for}\:{small}\:{variations}\:{in}\:{x} \\ $$$${if}\:{power}\:{doesn}'{t}\:{change}\:{much} \\ $$$${then}\:{for}\:{such}\:{a}\:{value}\:{of}\:{x} \\ $$$$\frac{{dP}_{{x}} }{{dx}}=\mathrm{0}\:;\:\Rightarrow\:\left({x}+\mathrm{36}\right)^{\mathrm{2}} =\mathrm{2}{x}\left({x}+\mathrm{36}\right) \\ $$$$\Rightarrow\:\:\:\:\:{x}\:=\:\mathrm{18}\:\Omega\:. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply