Menu Close

let-f-0-1-ln-1-e-i-x-dx-find-a-simple-form-of-f-

Tinku Tara 0 Comments
Pin




Question Number 36736 by abdo mathsup 649 cc last updated on 04/Jun/18
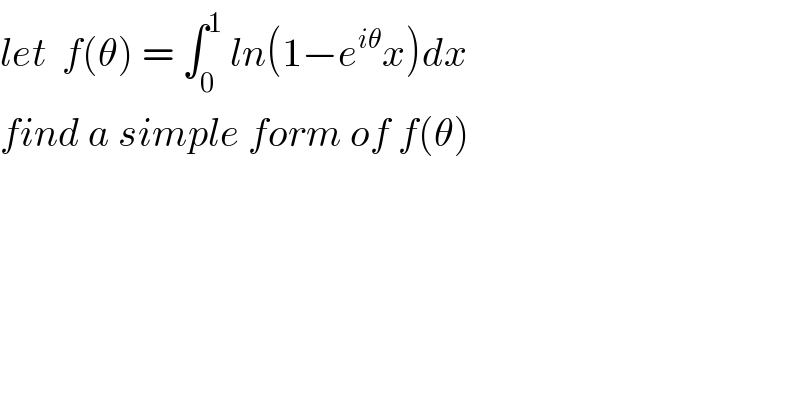
let f(θ) = ∫_0 ^1 ln(1−e^(iθ) x)dx find a simple form of f(θ)
$${let}\:\:{f}\left(\theta\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{e}^{{i}\theta} {x}\right){dx} \\ $$$${find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left(\theta\right) \\ $$
Commented by prof Abdo imad last updated on 06/Jun/18
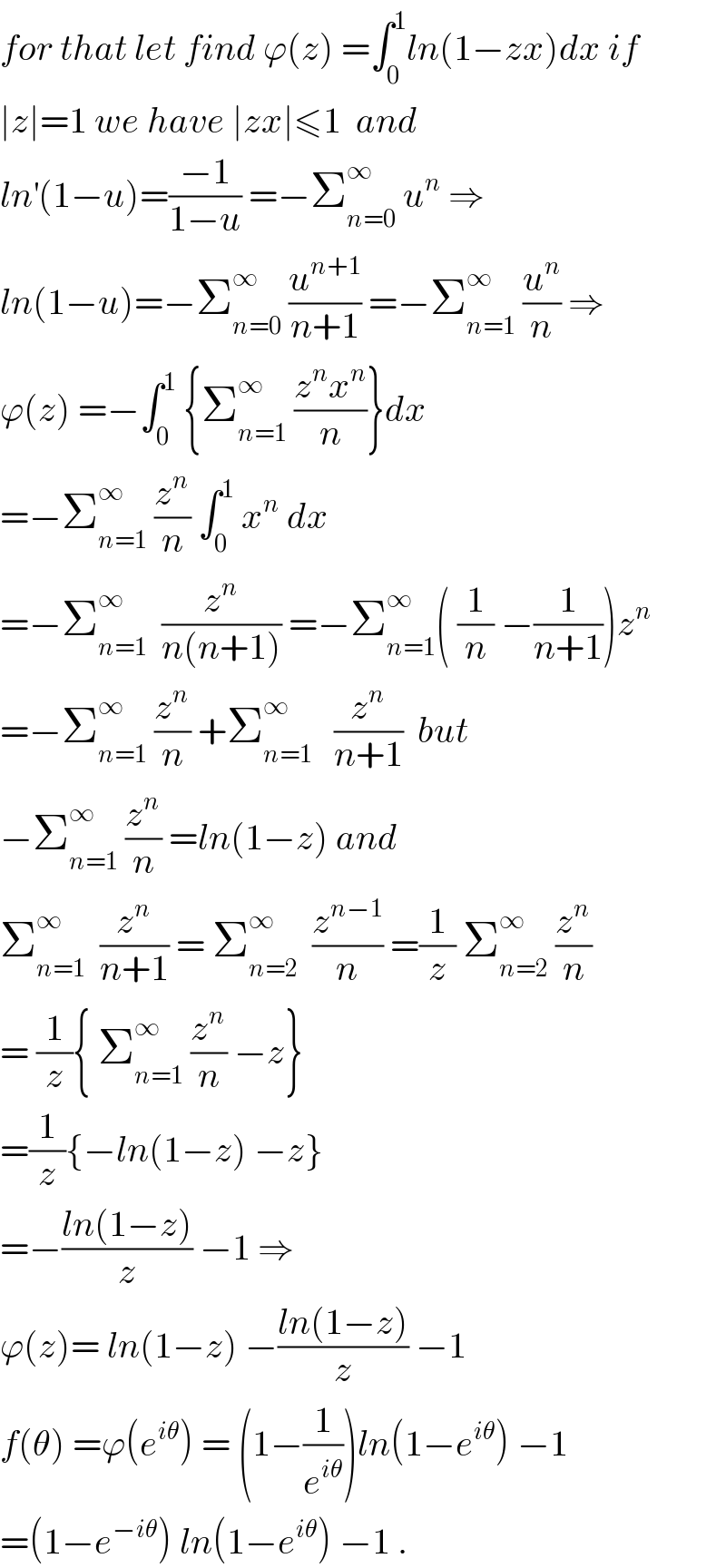
for that let find ϕ(z) =∫_0 ^1 ln(1−zx)dx if ∣z∣=1 we have ∣zx∣≤1 and ln^′ (1−u)=((−1)/(1−u)) =−Σ_(n=0) ^∞ u^n ⇒ ln(1−u)=−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (u^n /n) ⇒ ϕ(z) =−∫_0 ^1 {Σ_(n=1) ^∞ ((z^n x^n )/n)}dx =−Σ_(n=1) ^∞ (z^n /n) ∫_0 ^1 x^n dx =−Σ_(n=1) ^∞ (z^n /(n(n+1))) =−Σ_(n=1) ^∞ ( (1/n) −(1/(n+1)))z^n =−Σ_(n=1) ^∞ (z^n /n) +Σ_(n=1) ^∞ (z^n /(n+1)) but −Σ_(n=1) ^∞ (z^n /n) =ln(1−z) and Σ_(n=1) ^∞ (z^n /(n+1)) = Σ_(n=2) ^∞ (z^(n−1) /n) =(1/z) Σ_(n=2) ^∞ (z^n /n) = (1/z){ Σ_(n=1) ^∞ (z^n /n) −z} =(1/z){−ln(1−z) −z} =−((ln(1−z))/z) −1 ⇒ ϕ(z)= ln(1−z) −((ln(1−z))/z) −1 f(θ) =ϕ(e^(iθ) ) = (1−(1/e^(iθ) ))ln(1−e^(iθ) ) −1 =(1−e^(−iθ) ) ln(1−e^(iθ) ) −1 .
$${for}\:{that}\:{let}\:{find}\:\varphi\left({z}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{zx}\right){dx}\:{if} \\ $$$$\mid{z}\mid=\mathrm{1}\:{we}\:{have}\:\mid{zx}\mid\leqslant\mathrm{1}\:\:{and} \\ $$$${ln}^{'} \left(\mathrm{1}−{u}\right)=\frac{−\mathrm{1}}{\mathrm{1}−{u}}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{u}\right)=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\Rightarrow \\ $$$$\varphi\left({z}\right)\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\left\{\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}} {x}^{{n}} }{{n}}\right\}{dx} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:{dx} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{z}^{{n}} }{{n}\left({n}+\mathrm{1}\right)}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \left(\:\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right){z}^{{n}} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}} }{{n}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{{z}^{{n}} }{{n}+\mathrm{1}}\:\:{but} \\ $$$$−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}} }{{n}}\:={ln}\left(\mathrm{1}−{z}\right)\:{and} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{z}^{{n}} }{{n}+\mathrm{1}}\:=\:\sum_{{n}=\mathrm{2}} ^{\infty} \:\:\frac{{z}^{{n}−\mathrm{1}} }{{n}}\:=\frac{\mathrm{1}}{{z}}\:\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{z}^{{n}} }{{n}} \\ $$$$=\:\frac{\mathrm{1}}{{z}}\left\{\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}} }{{n}}\:−{z}\right\} \\ $$$$=\frac{\mathrm{1}}{{z}}\left\{−{ln}\left(\mathrm{1}−{z}\right)\:−{z}\right\} \\ $$$$=−\frac{{ln}\left(\mathrm{1}−{z}\right)}{{z}}\:−\mathrm{1}\:\Rightarrow \\ $$$$\varphi\left({z}\right)=\:{ln}\left(\mathrm{1}−{z}\right)\:−\frac{{ln}\left(\mathrm{1}−{z}\right)}{{z}}\:−\mathrm{1} \\ $$$${f}\left(\theta\right)\:=\varphi\left({e}^{{i}\theta} \right)\:=\:\left(\mathrm{1}−\frac{\mathrm{1}}{{e}^{{i}\theta} }\right){ln}\left(\mathrm{1}−{e}^{{i}\theta} \right)\:−\mathrm{1} \\ $$$$=\left(\mathrm{1}−{e}^{−{i}\theta} \right)\:{ln}\left(\mathrm{1}−{e}^{{i}\theta} \right)\:−\mathrm{1}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *