Solve-this-linear-Equation-dy-dx-y-cos-x-1-2-sin-x-

Question Number 102323 by Learner101 last updated on 08/Jul/20

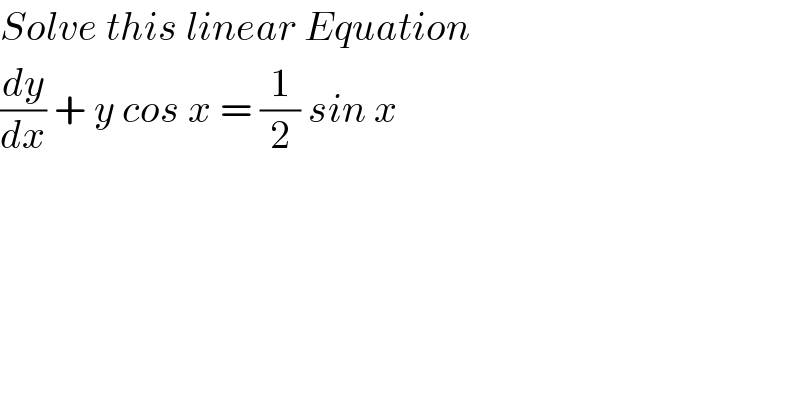
$${Solve}\:{this}\:{linear}\:{Equation} \\ $$$$\frac{{dy}}{{dx}}\:+\:{y}\:{cos}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:{sin}\:{x} \\ $$

Answered by bemath last updated on 08/Jul/20

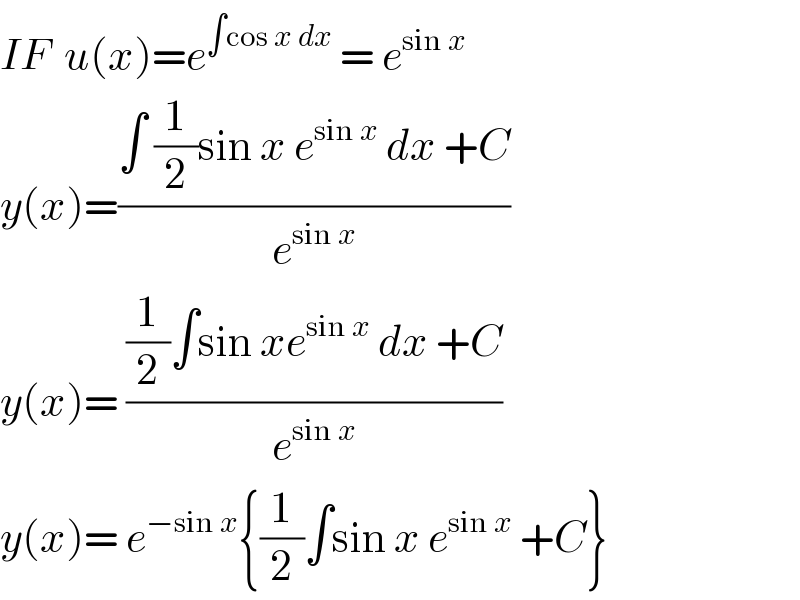
IF u(x)=e^(∫cos x dx) = e^(sin x) y(x)=((∫ (1/2)sin x e^(sin x) dx +C)/e^(sin x) ) y(x)= (((1/2)∫sin xe^(sin x) dx +C)/e^(sin x) ) y(x)= e^(−sin x) {(1/2)∫sin x e^(sin x) +C}

$${IF}\:\:{u}\left({x}\right)={e}^{\int\mathrm{cos}\:{x}\:{dx}} \:=\:{e}^{\mathrm{sin}\:{x}} \\ $$$${y}\left({x}\right)=\frac{\int\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{x}\:{e}^{\mathrm{sin}\:{x}} \:{dx}\:+{C}}{{e}^{\mathrm{sin}\:{x}} } \\ $$$${y}\left({x}\right)=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sin}\:{xe}^{\mathrm{sin}\:{x}} \:{dx}\:+{C}}{{e}^{\mathrm{sin}\:{x}} } \\ $$$${y}\left({x}\right)=\:{e}^{−\mathrm{sin}\:{x}} \left\{\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sin}\:{x}\:{e}^{\mathrm{sin}\:{x}} \:+{C}\right\} \\ $$

Commented by bemath last updated on 08/Jul/20

$${yes}\:{sir}.\: \\ $$

Answered by mathmax by abdo last updated on 08/Jul/20

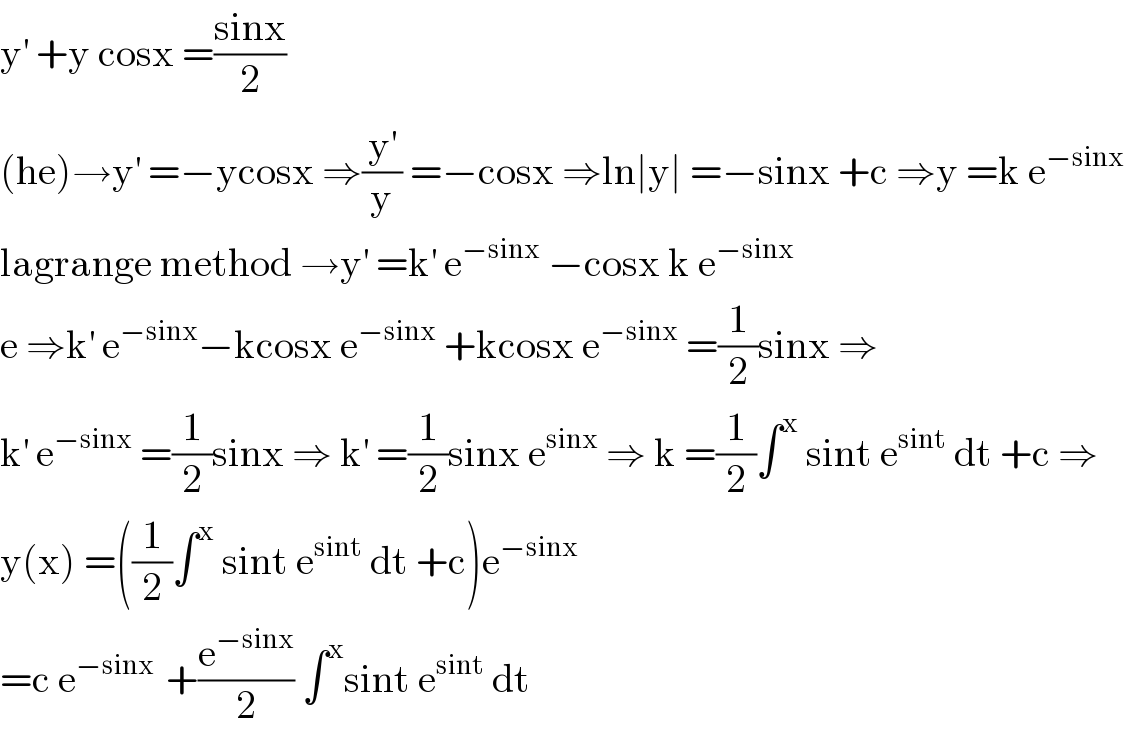
y^′ +y cosx =((sinx)/2) (he)→y^′ =−ycosx ⇒(y^′ /y) =−cosx ⇒ln∣y∣ =−sinx +c ⇒y =k e^(−sinx) lagrange method →y^′ =k^′ e^(−sinx) −cosx k e^(−sinx) e ⇒k^′ e^(−sinx) −kcosx e^(−sinx) +kcosx e^(−sinx) =(1/2)sinx ⇒ k^′ e^(−sinx) =(1/2)sinx ⇒ k^′ =(1/2)sinx e^(sinx) ⇒ k =(1/2)∫^x sint e^(sint) dt +c ⇒ y(x) =((1/2)∫^x sint e^(sint) dt +c)e^(−sinx) =c e^(−sinx ) +(e^(−sinx) /2) ∫^x sint e^(sint) dt

$$\mathrm{y}^{'} \:+\mathrm{y}\:\mathrm{cosx}\:=\frac{\mathrm{sinx}}{\mathrm{2}} \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{'} \:=−\mathrm{ycosx}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=−\mathrm{cosx}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=−\mathrm{sinx}\:+\mathrm{c}\:\Rightarrow\mathrm{y}\:=\mathrm{k}\:\mathrm{e}^{−\mathrm{sinx}} \\ $$$$\mathrm{lagrange}\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{sinx}} \:−\mathrm{cosx}\:\mathrm{k}\:\mathrm{e}^{−\mathrm{sinx}} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{sinx}} −\mathrm{kcosx}\:\mathrm{e}^{−\mathrm{sinx}} \:+\mathrm{kcosx}\:\mathrm{e}^{−\mathrm{sinx}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinx}\:\Rightarrow \\ $$$$\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{sinx}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinx}\:\Rightarrow\:\mathrm{k}^{'} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinx}\:\mathrm{e}^{\mathrm{sinx}} \:\Rightarrow\:\mathrm{k}\:=\frac{\mathrm{1}}{\mathrm{2}}\int^{\mathrm{x}} \:\mathrm{sint}\:\mathrm{e}^{\mathrm{sint}} \:\mathrm{dt}\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\int^{\mathrm{x}} \:\mathrm{sint}\:\mathrm{e}^{\mathrm{sint}} \:\mathrm{dt}\:+\mathrm{c}\right)\mathrm{e}^{−\mathrm{sinx}} \\ $$$$=\mathrm{c}\:\mathrm{e}^{−\mathrm{sinx}\:} \:+\frac{\mathrm{e}^{−\mathrm{sinx}} }{\mathrm{2}}\:\int^{\mathrm{x}} \mathrm{sint}\:\mathrm{e}^{\mathrm{sint}} \:\mathrm{dt} \\ $$

Facebook Tweet Pin

Solve-this-linear-Equation-dy-dx-y-cos-x-1-2-sin-x-

Leave a Reply Cancel reply