Question Number 102336 by 175mohamed last updated on 08/Jul/20
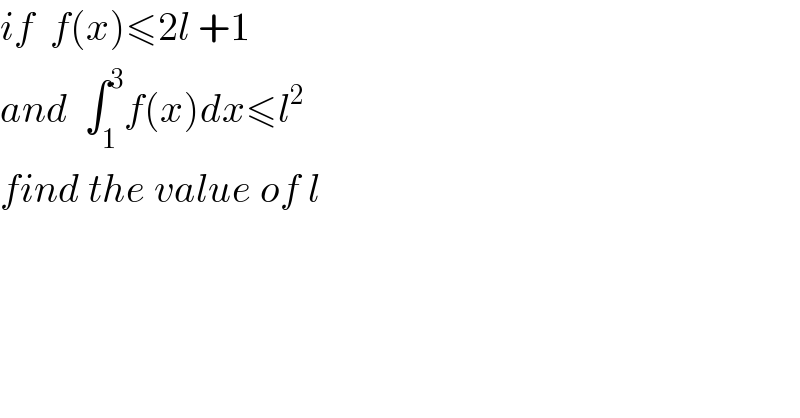
$${if}\:\:{f}\left({x}\right)\leqslant\mathrm{2}{l}\:+\mathrm{1}\: \\ $$$${and}\:\:\int_{\mathrm{1}} ^{\mathrm{3}} {f}\left({x}\right){dx}\leqslant{l}^{\mathrm{2}} \\ $$$${find}\:{the}\:{value}\:{of}\:{l} \\ $$
Commented by mr W last updated on 08/Jul/20
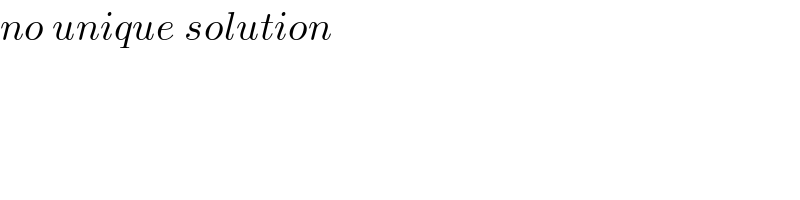
$${no}\:{unique}\:{solution} \\ $$
Answered by PRITHWISH SEN 2 last updated on 08/Jul/20
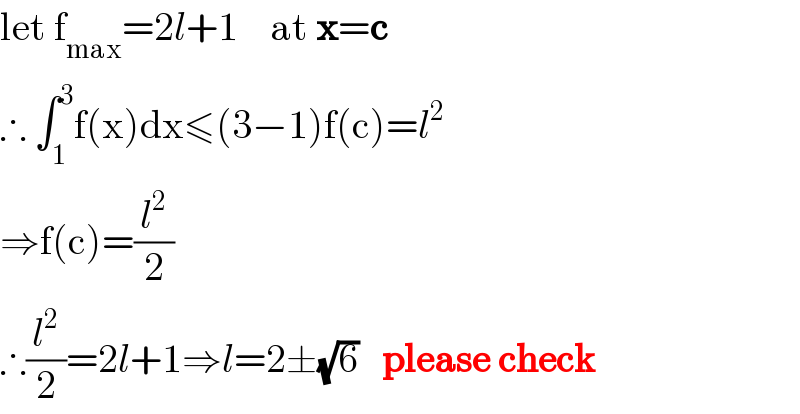
$$\mathrm{let}\:\mathrm{f}_{\mathrm{max}} =\mathrm{2}{l}+\mathrm{1}\:\:\:\:\mathrm{at}\:\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{c}} \\ $$$$\therefore\:\int_{\mathrm{1}} ^{\mathrm{3}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\leqslant\left(\mathrm{3}−\mathrm{1}\right)\mathrm{f}\left(\mathrm{c}\right)={l}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{c}\right)=\frac{{l}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\therefore\frac{{l}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2}{l}+\mathrm{1}\Rightarrow{l}=\mathrm{2}\pm\sqrt{\mathrm{6}}\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$
