Question Number 134662 by mnjuly1970 last updated on 06/Mar/21
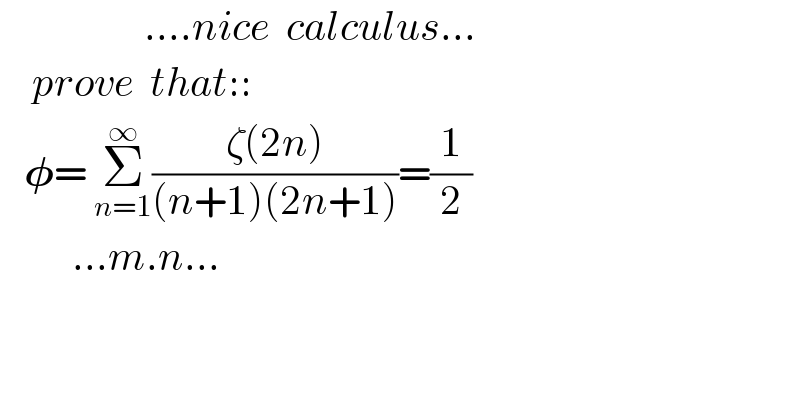
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….{nice}\:\:{calculus}… \\ $$$$\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\boldsymbol{\phi}=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{n}\right)}{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:…{m}.{n}… \\ $$
Answered by Dwaipayan Shikari last updated on 06/Mar/21
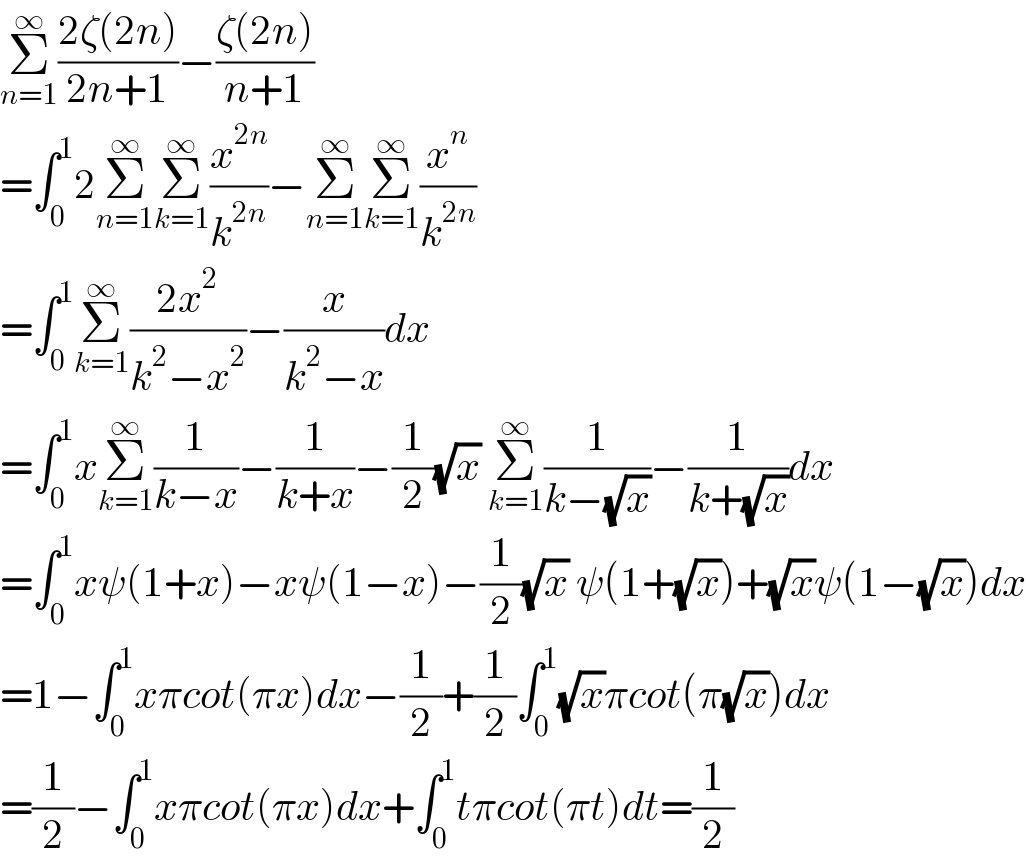
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}\zeta\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}+\mathrm{1}}−\frac{\zeta\left(\mathrm{2}{n}\right)}{{n}+\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{{k}^{\mathrm{2}{n}} }−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{k}^{\mathrm{2}{n}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} −{x}^{\mathrm{2}} }−\frac{{x}}{{k}^{\mathrm{2}} −{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}−{x}}−\frac{\mathrm{1}}{{k}+{x}}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}}\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}−\sqrt{{x}}}−\frac{\mathrm{1}}{{k}+\sqrt{{x}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\psi\left(\mathrm{1}+{x}\right)−{x}\psi\left(\mathrm{1}−{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}}\:\psi\left(\mathrm{1}+\sqrt{{x}}\right)+\sqrt{{x}}\psi\left(\mathrm{1}−\sqrt{{x}}\right){dx} \\ $$$$=\mathrm{1}−\int_{\mathrm{0}} ^{\mathrm{1}} {x}\pi{cot}\left(\pi{x}\right){dx}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}\pi{cot}\left(\pi\sqrt{{x}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\int_{\mathrm{0}} ^{\mathrm{1}} {x}\pi{cot}\left(\pi{x}\right){dx}+\int_{\mathrm{0}} ^{\mathrm{1}} {t}\pi{cot}\left(\pi{t}\right){dt}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 06/Mar/21

$${tayebballah}…{sir}\:\:{payan}… \\ $$$${your}\:{solution}\:{is}\:{very}\:{nice} \\ $$$$\:{and}\:{better}\:{than}\:{that}\:{me}.. \\ $$$${mercey}… \\ $$
Commented by mnjuly1970 last updated on 06/Mar/21
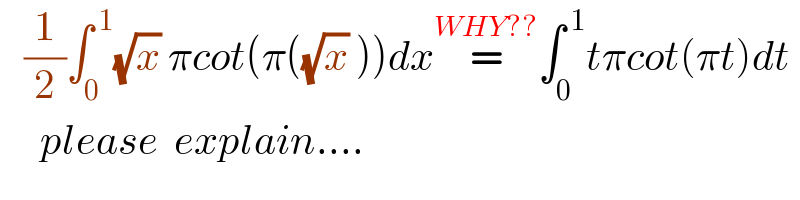
$$\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{{x}}\:\pi{cot}\left(\pi\left(\sqrt{{x}}\:\right)\right){dx}\overset{{WHY}??} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} {t}\pi{cot}\left(\pi{t}\right){dt} \\ $$$$\:\:\:\:\:{please}\:\:{explain}…. \\ $$
Answered by mnjuly1970 last updated on 07/Mar/21

Answered by mnjuly1970 last updated on 07/Mar/21

