Menu Close

Question-36880

Tinku Tara 0 Comments
Pin




Question Number 36880 by Tinkutara last updated on 06/Jun/18
Commented by ajfour last updated on 07/Jun/18
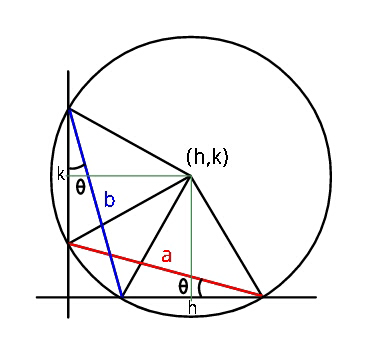
Commented by ajfour last updated on 07/Jun/18
2h=acos θ+bsin θ 2k=bcos θ+asin θ ⇒ cos θ=((2(ah−bk))/(a^2 −b^2 )) sin θ=((2(bh−ak))/(a^2 −b^2 )) so locus eq. is (ax−by)^2 +(bx−ay)^2 =(((a^2 −b^2 )^2 )/4) . doesn′t match with options..?!
$$\mathrm{2}{h}={a}\mathrm{cos}\:\theta+{b}\mathrm{sin}\:\theta \\ $$$$\mathrm{2}{k}={b}\mathrm{cos}\:\theta+{a}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta=\frac{\mathrm{2}\left({ah}−{bk}\right)}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\mathrm{sin}\:\theta=\frac{\mathrm{2}\left({bh}−{ak}\right)}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${so}\:{locus}\:{eq}.\:{is} \\ $$$$\left({ax}−{by}\right)^{\mathrm{2}} +\left({bx}−{ay}\right)^{\mathrm{2}} =\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}}\:. \\ $$$${doesn}'{t}\:{match}\:{with}\:{options}..?! \\ $$
Commented by Tinkutara last updated on 08/Jun/18
Sir please explain first 2 lines.
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jun/18
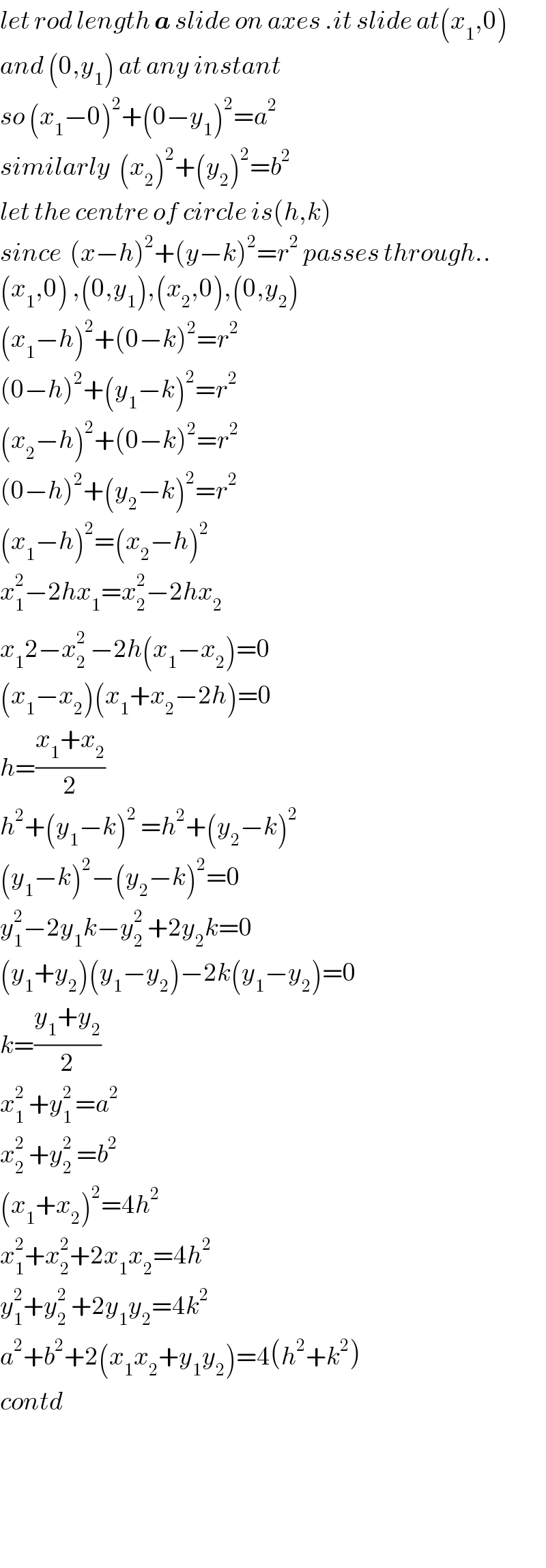
let rod length a slide on axes .it slide at(x_1 ,0) and (0,y_1 ) at any instant so (x_1 −0)^2 +(0−y_1 )^2 =a^2 similarly (x_2 )^2 +(y_2 )^2 =b^2 let the centre of circle is(h,k) since (x−h)^2 +(y−k)^2 =r^2 passes through..^ (x_1 ,0) ,(0,y_1 ),(x_2 ,0),(0,y_2 ) (x_1 −h)^2 +(0−k)^2 =r^2 (0−h)^2 +(y_1 −k)^2 =r^2 (x_2 −h)^2 +(0−k)^2 =r^2 (0−h)^2 +(y_2 −k)^2 =r^2 (x_1 −h)^2 =(x_2 −h)^2 x_1 ^2 −2hx_1 =x_2 ^2 −2hx_2 x_1 2−x_2 ^2 −2h(x_1 −x_2 )^ =0 (x_1 −x_2 )(x_1 +x_2 −2h)=0 h=((x_1 +x_2 )/2) h^2 +(y_1 −k)^2 =h^2 +(y_2 −k)^(2 ) (y_1 −k)^2 −(y_2 −k)^2 =0 y_1 ^2 −2y_1 k−y_2 ^2 +2y_2 k=0 (y_1 +y_2 )(y_1 −y_2 )−2k(y_1 −y_2 )=0 k=((y_1 +y_2 )/2) x_1 ^2 +y_1 ^(2 ) =a^2 x_2 ^2 +y_2 ^2 =b^2 (x_1 +x_2 )^2 =4h^2 x_1 ^2 +x_2 ^2 +2x_1 x_2 =4h^2 y_1 ^2 +y_2 ^2 +2y_1 y_2 =4k^2 a^2 +b^2 +2(x_1 x_2 +y_1 y_2 )=4(h^2 +k^2 ) contd
$${let}\:{rod}\:{length}\:\boldsymbol{{a}}\:{slide}\:{on}\:{axes}\:.{it}\:{slide}\:{at}\left({x}_{\mathrm{1}} ,\mathrm{0}\right)\: \\ $$$${and}\:\left(\mathrm{0},{y}_{\mathrm{1}} \right)\:{at}\:{any}\:{instant} \\ $$$${so}\:\left({x}_{\mathrm{1}} −\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{0}−{y}_{\mathrm{1}} \right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${similarly}\:\:\left({x}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}_{\mathrm{2}} \right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${let}\:{the}\:{centre}\:{of}\:{circle}\:{is}\left({h},{k}\right) \\ $$$${since}\:\:\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:{passes}\:{through}..^{} \\ $$$$\left({x}_{\mathrm{1}} ,\mathrm{0}\right)\:,\left(\mathrm{0},{y}_{\mathrm{1}} \right),\left({x}_{\mathrm{2}} ,\mathrm{0}\right),\left(\mathrm{0},{y}_{\mathrm{2}} \right) \\ $$$$\left({x}_{\mathrm{1}} −{h}\right)^{\mathrm{2}} +\left(\mathrm{0}−{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{0}−{h}\right)^{\mathrm{2}} +\left({y}_{\mathrm{1}} −{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{2}} −{h}\right)^{\mathrm{2}} +\left(\mathrm{0}−{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{0}−{h}\right)^{\mathrm{2}} +\left({y}_{\mathrm{2}} −{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{1}} −{h}\right)^{\mathrm{2}} =\left({x}_{\mathrm{2}} −{h}\right)^{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{hx}_{\mathrm{1}} ={x}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2}{hx}_{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} \mathrm{2}−{x}_{\mathrm{2}} ^{\mathrm{2}} \:−\mathrm{2}{h}\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \overset{} {\right)}=\mathrm{0} \\ $$$$\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} −\mathrm{2}{h}\right)=\mathrm{0} \\ $$$${h}=\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }{\mathrm{2}} \\ $$$${h}^{\mathrm{2}} +\left({y}_{\mathrm{1}} −{k}\right)^{\mathrm{2}} \:={h}^{\mathrm{2}} +\left({y}_{\mathrm{2}} −{k}\right)^{\mathrm{2}\:} \\ $$$$\left({y}_{\mathrm{1}} −{k}\right)^{\mathrm{2}} −\left({y}_{\mathrm{2}} −{k}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${y}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{y}_{\mathrm{1}} {k}−{y}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{2}{y}_{\mathrm{2}} {k}=\mathrm{0} \\ $$$$\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)\left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)−\mathrm{2}{k}\left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$${k}=\frac{{y}_{\mathrm{1}} +{y}_{\mathrm{2}} }{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{2}} \:+{y}_{\mathrm{1}} ^{\mathrm{2}\:} ={a}^{\mathrm{2}} \\ $$$${x}_{\mathrm{2}} ^{\mathrm{2}} \:+{y}_{\mathrm{2}} ^{\mathrm{2}} \:={b}^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{h}^{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{2}} =\mathrm{4}{h}^{\mathrm{2}} \\ $$$${y}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{2}{y}_{\mathrm{1}} {y}_{\mathrm{2}} =\mathrm{4}{k}^{\mathrm{2}} \: \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} +{y}_{\mathrm{1}} {y}_{\mathrm{2}} \right)=\mathrm{4}\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} \right) \\ $$$${contd} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *