Question Number 134678 by mr W last updated on 07/Mar/21

Commented by mr W last updated on 06/Mar/21

$${attempt}\:{to}\:{solve}\:{Q}\mathrm{134376} \\ $$
Commented by mr W last updated on 06/Mar/21
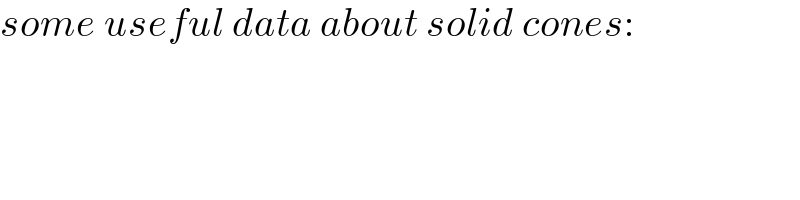
$${some}\:{useful}\:{data}\:{about}\:{solid}\:{cones}: \\ $$
Commented by mr W last updated on 06/Mar/21

Commented by mr W last updated on 07/Mar/21

Commented by mr W last updated on 07/Mar/21
![OC=axis of cone OD=contact line of cone on plane G=center of mass of cone OC=h OG=(3/4)h OD=(√(h^2 +r^2 )) tan ρ=(r/h) ⇒ρ=tan^(−1) (r/h) GE⊥OD GE=e=((OG)/(OD))×r=((3hr)/(4(√(h^2 +r^2 )))) OE=f=((OG)/(OD))×h=((3h^2 )/(4(√(h^2 +r^2 )))) the position of the cone is described through θ with −90°≤θ≤90°, since the cone is released from rest at θ=−90°. since the surface is rough enough such that the cone can only roll on the plane without slipping, the cone rotates about its tip point O along the plane. besides it rotates about its own axis OC. say the angular speed of the motion about O is ω_P and that about its axis is ω_a . ω_P =(dθ/dt)=ω since there is no slipping on the contact, OD×ω_P =r×ω_a ⇒ω_a =((OD)/r)ω_P =(ω/(sin ρ)) ω_(P,s) =ω_P cos ρ=ω cos ρ ω_(P,a) =−ω_P sin ρ=−ω sin ρ we see ω_(P,a) is opposite to ω_a , therefore the negative sign. I_a =((3mr^2 )/(10)) I_s =((3m)/(20))(r^2 +4h^2 ) the kinetic energy of cone at θ: KE_t =(1/2)I_a (ω_a +ω_(P,a) )^2 +(1/2)I_s ω_(P,s) ^2 KE_t =(1/2)×((3mr^2 )/(10))×((1/(sin ρ))−sin ρ)^2 ω^2 +(1/2)×((3m)/(20))(r^2 +4h^2 )×cos^2 ρ×ω^2 KE_t =((3m)/(40))[((2/(sin ρ))−sin ρ)((1/(sin ρ))−sin ρ)r^2 +4 cos^2 ρ h^2 ]ω^2 KE_t =((3mh^2 )/(40))[((2/(sin ρ))−sin ρ)((1/(sin ρ))−sin ρ)tan^2 ρ+4 cos^2 ρ]ω^2 KE_t =((3mh^2 )/(40))(1+5 cos^2 ρ)ω^2 let z_O =0 at t=0 and θ=−90°: z_(E,0) =0 at θ: z_(E,t) =−OE×cos θ×sin φ=−f cos θ sin φ KE_t =mg(z_(E,0) −z_(E,t) ) ((3mh^2 )/(40))(1+5 cos^2 ρ)ω^2 =mgf cos θ sin φ (1+5 cos^2 ρ)ω^2 =((10g)/( (√(h^2 +r^2 ))))×cos θ sin φ ω^2 =((10g cos ρ)/( h(1+5 cos^2 ρ)))×cos θ sin φ with ξ=(√((10g cos ρ)/( h(1+5 cos^2 ρ)))) ⇒ω=ξ(√(sin φ cos θ)) (dθ/dt)=ξ(√(sin φ cos θ)) ∫(dθ/( (√(cos θ))))=ξ(√(sin φ))∫dt let T=period ∫_0 ^(π/2) (dθ/( (√(cos θ))))=((ξ(√(sin φ)) T)/4) ⇒T=(4/(ξ(√(sin φ))))∫_0 ^(π/2) (dθ/( (√(cos θ))))=((2B((1/4),(1/2)))/(ξ(√(sin φ)))) ⇒T≈((10.48823)/(ξ(√(sin φ))))=3.31667(√((1+5 cos^2 ρ)/(cos ρ sin φ)))(√(h/g)) example: ρ=15°=(π/(12)) φ=30°=(π/6) T≈11.359(√(h/g))](https://www.tinkutara.com/question/Q134685.png)
$${OC}={axis}\:{of}\:{cone} \\ $$$${OD}={contact}\:{line}\:{of}\:{cone}\:{on}\:{plane} \\ $$$${G}={center}\:{of}\:{mass}\:{of}\:{cone} \\ $$$${OC}={h} \\ $$$${OG}=\frac{\mathrm{3}}{\mathrm{4}}{h} \\ $$$${OD}=\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\rho=\frac{{r}}{{h}}\:\Rightarrow\rho=\mathrm{tan}^{−\mathrm{1}} \frac{{r}}{{h}} \\ $$$${GE}\bot{OD} \\ $$$${GE}={e}=\frac{{OG}}{{OD}}×{r}=\frac{\mathrm{3}{hr}}{\mathrm{4}\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} }} \\ $$$${OE}={f}=\frac{{OG}}{{OD}}×{h}=\frac{\mathrm{3}{h}^{\mathrm{2}} }{\mathrm{4}\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} }} \\ $$$$ \\ $$$${the}\:{position}\:{of}\:{the}\:{cone}\:{is}\:{described} \\ $$$${through}\:\theta\:{with}\:−\mathrm{90}°\leqslant\theta\leqslant\mathrm{90}°,\:{since} \\ $$$${the}\:{cone}\:{is}\:{released}\:{from}\:{rest}\:{at} \\ $$$$\theta=−\mathrm{90}°. \\ $$$${since}\:{the}\:{surface}\:{is}\:{rough}\:{enough} \\ $$$${such}\:{that}\:{the}\:{cone}\:{can}\:{only}\:{roll} \\ $$$${on}\:{the}\:{plane}\:{without}\:{slipping}, \\ $$$${the}\:{cone}\:{rotates}\:{about}\:{its}\:{tip}\:{point}\:{O} \\ $$$${along}\:{the}\:{plane}.\:{besides}\:{it}\:{rotates} \\ $$$${about}\:{its}\:{own}\:{axis}\:{OC}.\:{say}\:{the} \\ $$$${angular}\:{speed}\:{of}\:{the}\:{motion}\:{about}\:{O} \\ $$$${is}\:\omega_{{P}} \:{and}\:{that}\:{about}\:{its}\:{axis}\:{is}\:\omega_{{a}} . \\ $$$$\omega_{{P}} =\frac{{d}\theta}{{dt}}=\omega \\ $$$${since}\:{there}\:{is}\:{no}\:{slipping}\:{on}\:{the} \\ $$$${contact},\: \\ $$$${OD}×\omega_{{P}} ={r}×\omega_{{a}} \\ $$$$\Rightarrow\omega_{{a}} =\frac{{OD}}{{r}}\omega_{{P}} =\frac{\omega}{\mathrm{sin}\:\rho} \\ $$$$\omega_{{P},{s}} =\omega_{{P}} \mathrm{cos}\:\rho=\omega\:\mathrm{cos}\:\rho \\ $$$$\omega_{{P},{a}} =−\omega_{{P}} \mathrm{sin}\:\rho=−\omega\:\mathrm{sin}\:\rho \\ $$$${we}\:{see}\:\omega_{{P},{a}} \:{is}\:{opposite}\:{to}\:\omega_{{a}} ,\:{therefore} \\ $$$${the}\:{negative}\:{sign}. \\ $$$${I}_{{a}} =\frac{\mathrm{3}{mr}^{\mathrm{2}} }{\mathrm{10}} \\ $$$${I}_{{s}} =\frac{\mathrm{3}{m}}{\mathrm{20}}\left({r}^{\mathrm{2}} +\mathrm{4}{h}^{\mathrm{2}} \right) \\ $$$${the}\:{kinetic}\:{energy}\:{of}\:{cone}\:{at}\:\theta: \\ $$$${KE}_{{t}} =\frac{\mathrm{1}}{\mathrm{2}}{I}_{{a}} \left(\omega_{{a}} +\omega_{{P},{a}} \right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{I}_{{s}} \omega_{{P},{s}} ^{\mathrm{2}} \\ $$$${KE}_{{t}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}{mr}^{\mathrm{2}} }{\mathrm{10}}×\left(\frac{\mathrm{1}}{\mathrm{sin}\:\rho}−\mathrm{sin}\:\rho\right)^{\mathrm{2}} \omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}{m}}{\mathrm{20}}\left({r}^{\mathrm{2}} +\mathrm{4}{h}^{\mathrm{2}} \right)×\mathrm{cos}^{\mathrm{2}} \:\rho×\omega^{\mathrm{2}} \\ $$$${KE}_{{t}} =\frac{\mathrm{3}{m}}{\mathrm{40}}\left[\left(\frac{\mathrm{2}}{\mathrm{sin}\:\rho}−\mathrm{sin}\:\rho\right)\left(\frac{\mathrm{1}}{\mathrm{sin}\:\rho}−\mathrm{sin}\:\rho\right){r}^{\mathrm{2}} +\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\rho\:{h}^{\mathrm{2}} \right]\omega^{\mathrm{2}} \\ $$$${KE}_{{t}} =\frac{\mathrm{3}{mh}^{\mathrm{2}} }{\mathrm{40}}\left[\left(\frac{\mathrm{2}}{\mathrm{sin}\:\rho}−\mathrm{sin}\:\rho\right)\left(\frac{\mathrm{1}}{\mathrm{sin}\:\rho}−\mathrm{sin}\:\rho\right)\mathrm{tan}^{\mathrm{2}} \:\rho+\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\rho\right]\omega^{\mathrm{2}} \\ $$$${KE}_{{t}} =\frac{\mathrm{3}{mh}^{\mathrm{2}} }{\mathrm{40}}\left(\mathrm{1}+\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\rho\right)\omega^{\mathrm{2}} \\ $$$${let}\:{z}_{{O}} =\mathrm{0} \\ $$$${at}\:{t}=\mathrm{0}\:{and}\:\theta=−\mathrm{90}°: \\ $$$${z}_{{E},\mathrm{0}} =\mathrm{0} \\ $$$${at}\:\theta: \\ $$$${z}_{{E},{t}} =−{OE}×\mathrm{cos}\:\theta×\mathrm{sin}\:\phi=−{f}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\phi \\ $$$${KE}_{{t}} ={mg}\left({z}_{{E},\mathrm{0}} −{z}_{{E},{t}} \right) \\ $$$$\frac{\mathrm{3}{mh}^{\mathrm{2}} }{\mathrm{40}}\left(\mathrm{1}+\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\rho\right)\omega^{\mathrm{2}} ={mgf}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\phi \\ $$$$\left(\mathrm{1}+\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\rho\right)\omega^{\mathrm{2}} =\frac{\mathrm{10}{g}}{\:\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} }}×\mathrm{cos}\:\theta\:\mathrm{sin}\:\phi \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{10}{g}\:\mathrm{cos}\:\rho}{\:{h}\left(\mathrm{1}+\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\rho\right)}×\mathrm{cos}\:\theta\:\mathrm{sin}\:\phi \\ $$$${with}\:\xi=\sqrt{\frac{\mathrm{10}{g}\:\mathrm{cos}\:\rho}{\:{h}\left(\mathrm{1}+\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\rho\right)}} \\ $$$$\Rightarrow\omega=\xi\sqrt{\mathrm{sin}\:\phi\:\mathrm{cos}\:\theta} \\ $$$$\frac{{d}\theta}{{dt}}=\xi\sqrt{\mathrm{sin}\:\phi\:\mathrm{cos}\:\theta} \\ $$$$\int\frac{{d}\theta}{\:\sqrt{\mathrm{cos}\:\theta}}=\xi\sqrt{\mathrm{sin}\:\phi}\int{dt} \\ $$$${let}\:{T}={period} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\theta}{\:\sqrt{\mathrm{cos}\:\theta}}=\frac{\xi\sqrt{\mathrm{sin}\:\phi}\:{T}}{\mathrm{4}} \\ $$$$\Rightarrow{T}=\frac{\mathrm{4}}{\xi\sqrt{\mathrm{sin}\:\phi}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\theta}{\:\sqrt{\mathrm{cos}\:\theta}}=\frac{\mathrm{2}{B}\left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{2}}\right)}{\xi\sqrt{\mathrm{sin}\:\phi}} \\ $$$$\Rightarrow{T}\approx\frac{\mathrm{10}.\mathrm{48823}}{\xi\sqrt{\mathrm{sin}\:\phi}}=\mathrm{3}.\mathrm{31667}\sqrt{\frac{\mathrm{1}+\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\rho}{\mathrm{cos}\:\rho\:\mathrm{sin}\:\phi}}\sqrt{\frac{{h}}{{g}}} \\ $$$$ \\ $$$${example}: \\ $$$$\rho=\mathrm{15}°=\frac{\pi}{\mathrm{12}} \\ $$$$\phi=\mathrm{30}°=\frac{\pi}{\mathrm{6}} \\ $$$${T}\approx\mathrm{11}.\mathrm{359}\sqrt{\frac{{h}}{{g}}} \\ $$
Commented by physicstutes last updated on 06/Mar/21

$$\mathrm{sir}\:\mathrm{W}\:\mathrm{please}\:\mathrm{reference}\:\mathrm{me}\:\mathrm{to}\:\mathrm{an}\:\mathrm{e}−\mathrm{book}\:\mathrm{where} \\ $$$$\mathrm{i}\:\mathrm{can}\:\mathrm{learn}\:\mathrm{basic}\:\mathrm{moment}\:\mathrm{of}\:\mathrm{inertia},\:\mathrm{especially}\:\mathrm{things} \\ $$$$\mathrm{like}\:\mathrm{basic}\:\mathrm{integral}\:\mathrm{derivation}\:\mathrm{of}\:\mathrm{moment}\:\mathrm{of}\:\mathrm{inertia} \\ $$$$\mathrm{for}\:\mathrm{certain}\:\mathrm{shapes}\left(\mathrm{like}\:\mathrm{rods},\mathrm{rectangles},\:\mathrm{rings}\:\mathrm{etc}\right)\:\mathrm{and} \\ $$$$\mathrm{appling}\:\mathrm{these}\:\mathrm{knowledge}\:\mathrm{to}\:\mathrm{compound}\:\mathrm{pendulum}\:\mathrm{and}\:\mathrm{swinging} \\ $$$$\mathrm{masses}.\:\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{help}\:\mathrm{with}\:\mathrm{those}.\: \\ $$
Commented by mr W last updated on 06/Mar/21

$${i}\:{really}\:{don}'{t}\:{know}\:{such}\:{a}\:{book}\:{which} \\ $$$${i}\:{can}\:{recommend}.\:{nowadays}\:{when}\:{i} \\ $$$${need}\:{to}\:{look}\:{something},\:{i}\:{just}\:{google}. \\ $$
Commented by I want to learn more last updated on 06/Mar/21

$$\mathrm{weldone}\:\mathrm{sir}. \\ $$
Commented by physicstutes last updated on 06/Mar/21

$$\mathrm{i}\:\mathrm{tried}\:\mathrm{googling}\:\mathrm{but}\:\mathrm{could}\:\mathrm{not}\:\mathrm{find}\:\mathrm{a}\:\mathrm{suitable}\: \\ $$$$\mathrm{pdf}\:\mathrm{or}\:\mathrm{even}\:\mathrm{a}\:\mathrm{book}\:\mathrm{for}\:\mathrm{the}\:\mathrm{assesment}. \\ $$
