Menu Close

find-lim-n-k-1-n-1-k-n-2-

Tinku Tara 0 Comments
Pin




Question Number 36925 by maxmathsup by imad last updated on 07/Jun/18
find lim_(n→+∞) Π_(k=1) ^n (1+(k/n^2 )).
$${find}\:{lim}_{{n}\rightarrow+\infty} \:\prod_{{k}=\mathrm{1}} ^{{n}} \:\:\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right). \\ $$
Commented by math khazana by abdo last updated on 26/Jun/18
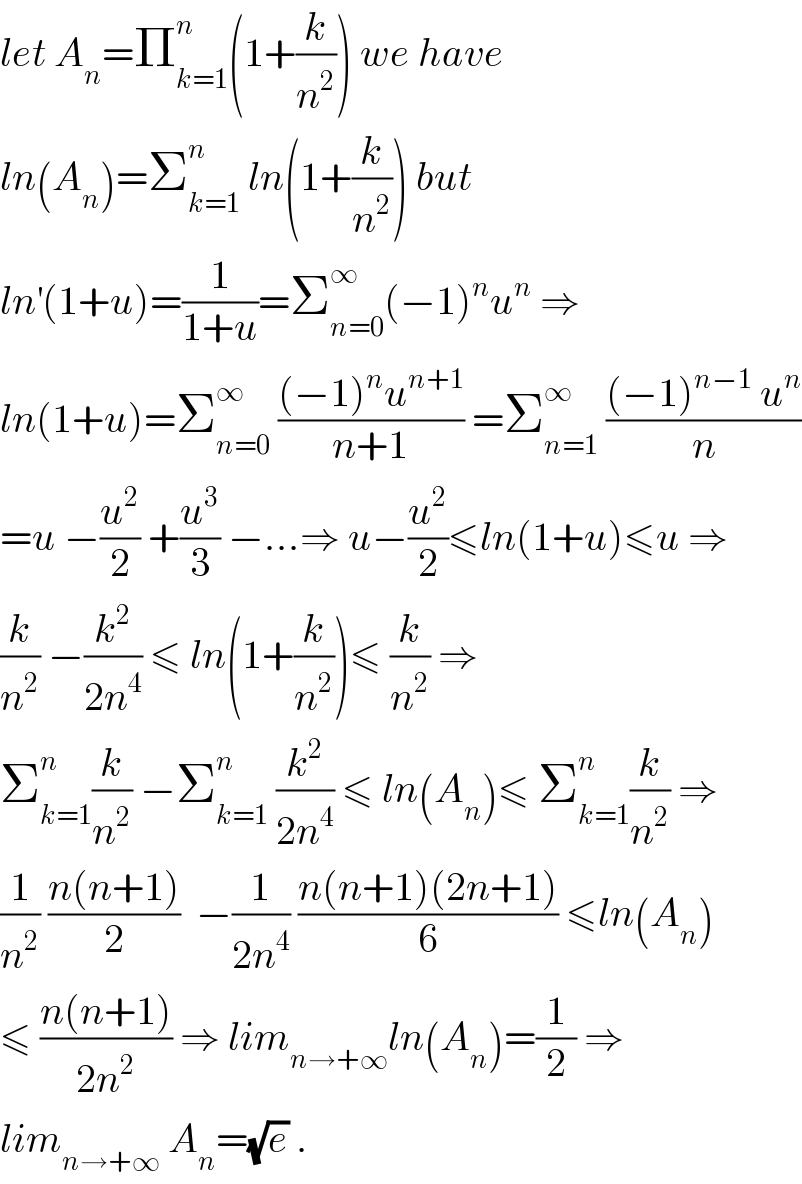
let A_n =Π_(k=1) ^n (1+(k/n^2 )) we have ln(A_n )=Σ_(k=1) ^n ln(1+(k/n^2 )) but ln^′ (1+u)=(1/(1+u))=Σ_(n=0) ^∞ (−1)^n u^n ⇒ ln(1+u)=Σ_(n=0) ^∞ (((−1)^n u^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) u^n )/n) =u −(u^2 /2) +(u^3 /3) −...⇒ u−(u^2 /2)≤ln(1+u)≤u ⇒ (k/n^2 ) −(k^2 /(2n^4 )) ≤ ln(1+(k/n^2 ))≤ (k/n^2 ) ⇒ Σ_(k=1) ^n (k/n^2 ) −Σ_(k=1) ^n (k^2 /(2n^4 )) ≤ ln(A_n )≤ Σ_(k=1) ^n (k/n^2 ) ⇒ (1/n^2 ) ((n(n+1))/2) −(1/(2n^4 )) ((n(n+1)(2n+1))/6) ≤ln(A_n ) ≤ ((n(n+1))/(2n^2 )) ⇒ lim_(n→+∞) ln(A_n )=(1/2) ⇒ lim_(n→+∞) A_n =(√e) .
$${let}\:{A}_{{n}} =\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\:{we}\:{have}\: \\ $$$${ln}\left({A}_{{n}} \right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:{ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\:{but} \\ $$$${ln}^{'} \left(\mathrm{1}+{u}\right)=\frac{\mathrm{1}}{\mathrm{1}+{u}}=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{u}^{{n}} }{{n}} \\ $$$$={u}\:−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{u}^{\mathrm{3}} }{\mathrm{3}}\:−…\Rightarrow\:{u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\leqslant{ln}\left(\mathrm{1}+{u}\right)\leqslant{u}\:\Rightarrow \\ $$$$\frac{{k}}{{n}^{\mathrm{2}} }\:−\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\:\leqslant\:{ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\leqslant\:\frac{{k}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \frac{{k}}{{n}^{\mathrm{2}} }\:−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\:\leqslant\:{ln}\left({A}_{{n}} \right)\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} \frac{{k}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }\:\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\:\leqslant{ln}\left({A}_{{n}} \right) \\ $$$$\leqslant\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} {ln}\left({A}_{{n}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\sqrt{{e}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *