Question Number 102474 by pticantor last updated on 09/Jul/20
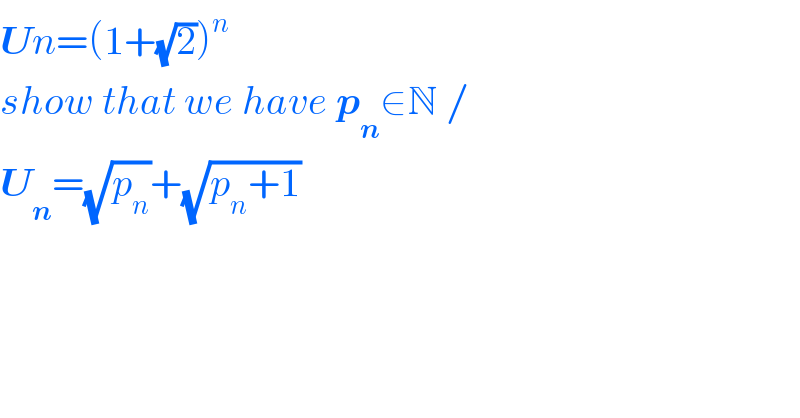
$$\boldsymbol{{U}}{n}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{n}} \\ $$$${show}\:{that}\:{we}\:{have}\:\boldsymbol{{p}}_{\boldsymbol{{n}}} \in\mathbb{N}\:/ \\ $$$$\boldsymbol{{U}}_{\boldsymbol{{n}}} =\sqrt{{p}_{{n}} }+\sqrt{{p}_{{n}} +\mathrm{1}} \\ $$
Answered by ~blr237~ last updated on 09/Jul/20

$$\:{observe}\:{that}\:\frac{\mathrm{1}}{{U}_{{n}} }=\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{{n}} \:\:{and}\:{that}\:{there}\:{exist}\: \\ $$$${a}_{{n}} \:,{b}_{{n}} \in\mathbb{N}\:\:{such}\:{as}\:\:\:{U}_{{n}} ={a}_{{n}} +{b}_{{n}} \sqrt{\mathrm{2}}\:\:\:\:{and}\:\:\frac{\mathrm{1}}{{U}_{{n}} }=\left(−\mathrm{1}\right)^{{n}} \left({a}_{{n}} −{b}_{{n}} \sqrt{\mathrm{2}}\right) \\ $$$${and}\:\:{U}_{{n}} ^{\mathrm{2}} ={U}_{\mathrm{2}{n}} \:. \\ $$$${So}\:\:\left({U}_{{n}} ^{} +\frac{\mathrm{1}}{{U}_{{n}} }\right)^{\mathrm{2}} =\:\mathrm{2}+{U}_{\mathrm{2}{n}} +\frac{\mathrm{1}}{{U}_{\mathrm{2}{n}} }=\mathrm{2}\:+\mathrm{2}{a}_{\mathrm{2}{n}} \: \\ $$$$\left({U}_{{n}} −\frac{\mathrm{1}}{{U}_{{n}} }\right)^{\mathrm{2}} =−\mathrm{2}+{U}_{\mathrm{2}{n}} +\frac{\mathrm{1}}{{U}_{\mathrm{2}{n}} }\:=−\mathrm{2}+\mathrm{2}{a}_{\mathrm{2}{n}} \\ $$$${we}\:{have}\:\:{a}_{{n}+\mathrm{1}} +{b}_{{n}+\mathrm{1}} \sqrt{\mathrm{2}}\:=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({a}_{{n}} +{b}_{{n}} \sqrt{\mathrm{2}}\:\right)\:{lead}\:{to} \\ $$$${a}_{{n}+\mathrm{1}} ={a}_{{n}} +\mathrm{2}{b}_{{n}} \:.\:{So}\:\:{such}\:{as}\:{a}_{\mathrm{1}} =\mathrm{1}\:\left({odd}\:\right)\:,\:{a}_{{n}} \:{is}\:{always}\:{odd}\: \\ $$$${So}\:{there}\:{exist}\:\:{c}_{{n}} \:\in\mathbb{N}\:\:/\:{a}_{{n}} =\mathrm{2}{c}_{{n}} +\mathrm{1} \\ $$$${Then}\:\:\:\:\left({U}_{{n}} +\frac{\mathrm{1}}{{U}_{{n}} }\right)^{\mathrm{2}} =\mathrm{2}+\mathrm{2}\left(\mathrm{2}{c}_{\mathrm{2}{n}} +\mathrm{1}\right)=\mathrm{4}\left({c}_{\mathrm{2}{n}} +\mathrm{1}\right) \\ $$$$\:\left({U}_{{n}} −\frac{\mathrm{1}}{{U}_{{n}} }\right)^{\mathrm{2}} =−\mathrm{2}+\mathrm{2}\left(\mathrm{2}{c}_{\mathrm{2}{n}} +\mathrm{1}\right)=\mathrm{4}{c}_{\mathrm{2}{n}} \: \\ $$$${By}\:{adding}\:{the}\:{two}\:{square}\:{root}\: \\ $$$${U}_{{n}} =\sqrt{{c}_{\mathrm{2}{n}} }\:+\sqrt{{c}_{\mathrm{2}{n}} +\mathrm{1}}\:\:\:\:{take}\:\:{p}_{{n}} ={c}_{\mathrm{2}{n}} \\ $$$$ \\ $$$$ \\ $$
