Question Number 36942 by maxmathsup by imad last updated on 07/Jun/18
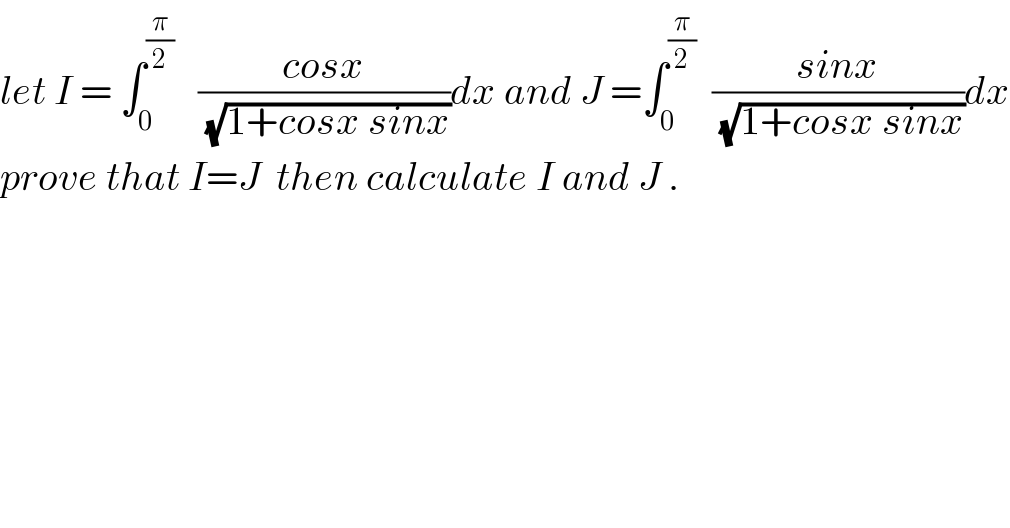
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{cosx}}{\:\sqrt{\mathrm{1}+{cosx}\:{sinx}}}{dx}\:{and}\:{J}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sinx}}{\:\sqrt{\mathrm{1}+{cosx}\:{sinx}}}{dx} \\ $$$${prove}\:{that}\:{I}={J}\:\:{then}\:{calculate}\:{I}\:{and}\:{J}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Jun/18

$${I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{cosx}}{\:\sqrt{\mathrm{1}+{cosxsinx}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{cos}\left(\frac{\Pi}{\mathrm{2}}−{x}\right)}{\:\sqrt{\mathrm{1}+{cos}\left(\frac{\Pi}{\mathrm{2}}−{x}\right){sin}\left(\frac{\Pi}{\mathrm{2}}−{x}\right)}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \:\frac{{sinx}}{\:\sqrt{\mathrm{1}+{sinxcosx}}}{dx} \\ $$$$={J}\:\left({provd}\right) \\ $$$${I}+{J}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{cosx}+{sinx}}{\:\sqrt{\mathrm{1}+{sinxcosx}}}{dx} \\ $$$$=\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \:\frac{{cosx}+{sinx}}{\:\sqrt{\mathrm{1}+\mathrm{1}+\mathrm{2}{sinxcosx}}}{dx} \\ $$$$=\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{d}\left({sinx}−{cosx}\right)}{\:\sqrt{\mathrm{1}−\left(−\mathrm{1}−\mathrm{2}{sinxcosx}\right)}} \\ $$$$=\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \:\frac{{d}\left({sinx}−{cosx}\right)}{\:\sqrt{\mathrm{1}−\left(−\mathrm{2}+\mathrm{1}−\mathrm{2}{sinxcosx}\right)}} \\ $$$$\sqrt{}\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{d}\left({sinx}−{cosx}\right)}{\:\sqrt{\mathrm{3}−\left({sinx}−{cosx}\right)^{\mathrm{2}} }}\:\:\:\:\left[\int\frac{{dx}}{\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}={sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)\right. \\ $$$$=\sqrt{\mathrm{2}}\:×\mid{sin}^{−\mathrm{1}} \left(\frac{{sinx}−{cosx}}{\:\sqrt{\mathrm{3}}}\right)\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \\ $$$$=\sqrt{\mathrm{2}}\:×\left\{{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−{sin}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right\} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\:{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$${I}+{j}=\mathrm{2}{I}=\mathrm{2}\sqrt{\mathrm{2}}\:{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\:}\right) \\ $$$${I}={J}=\sqrt{\mathrm{2}}\:{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$
