Question Number 36980 by Tinkutara last updated on 07/Jun/18
Answered by tanmay.chaudhury50@gmail.com last updated on 08/Jun/18

$${charge}\:{densigy}=\lambda \\ $$$${let}\:{length}\:{of}\:{rod}={l}=\mathrm{10}{cm} \\ $$$${distance}\:{of}\:{point}\:{p}\:{from}\:{the}\:{centre}\:{of}\:{rod}\:{is} \\ $$$${h}=\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}{l}….{as}\:{per}\:{question}\:{point}\:{p}\:{and}\:{two}\: \\ $$$${end}\:{of}\:{rods}\:{make}\:{a}\:{equilateral}\:\:{triangle} \\ $$$${from}\:{centre}\:{of}\:{rod}\:{along}\:{the}\:{length}\:{lf}\:{rod} \\ $$$${at}\:{adistance}\:{x}\:{se}\:{takda}\:{small}\:{strip} \\ $$$${dx}. \\ $$$${the}\:{charge}\:{in}\:{dx}\:{element}\:{is}=\lambda{dx} \\ $$$${electric}\:{field}\:{dE}=\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\frac{\lambda{dx}}{\left(\sqrt{\left.{h}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right.}\: \\ $$$${effectivedE}=\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\frac{\lambda{dx}}{\left(\sqrt{\left.{h}_{} ^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right.}{cos}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\left(\frac{\lambda{hdx}}{\left({h}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)\frac{\mathrm{3}}{\mathrm{2}}}\:\:\:\:\:{when}\:{cos}\theta=\left(\frac{{h}}{\:\sqrt{{h}^{\mathrm{2}} +{x}^{\mathrm{3}} }}\right)\right. \\ $$$${E}\:{effective}.\:\:=\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }\int_{−\frac{{l}}{\mathrm{2}}} ^{\frac{{l}}{\mathrm{2}}} \frac{\lambda{hdx}}{\left({h}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{\lambda{h}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }\int_{−\frac{{l}}{\mathrm{2}}} ^{\frac{{l}}{\mathrm{2}}} \frac{{dx}}{\left({h}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }……{eqn}\mathrm{1} \\ $$$$ \\ $$$${x}={htan}\theta\:\:\:{dx}={hsec}^{\mathrm{2}} \theta{d}\theta \\ $$$${let}\:{I}=\int\frac{{dx}}{\left({h}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\int\frac{{hsec}^{\mathrm{2}} \theta{d}\theta}{{h}^{\mathrm{3}} {sec}^{\mathrm{3}} \theta} \\ $$$$=\frac{\mathrm{1}}{{h}^{\mathrm{2}} }\int{cos}\theta{d}\theta \\ $$$$=\frac{\mathrm{1}}{{h}^{\mathrm{2}} }{sin}\theta \\ $$$$=\frac{\mathrm{1}}{{h}^{\mathrm{2}} }\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{h}^{\mathrm{2}} }} \\ $$$$=\frac{\lambda{h}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\frac{\mathrm{1}}{{h}^{\mathrm{2}} }\mid\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{h}^{\mathrm{2}} }}\mid_{\frac{−{l}}{\mathrm{2}}} ^{\frac{{l}}{\mathrm{2}}} \:\: \\ $$$$=\frac{\lambda}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} {h}}×\left\{\frac{\frac{{l}}{\mathrm{2}}}{\:\sqrt{\frac{{l}^{\mathrm{2}} }{\mathrm{4}}+{h}^{\mathrm{2}} }}−\frac{\frac{−{l}}{\mathrm{2}}}{\:\sqrt{\frac{{l}^{\mathrm{2}} }{\mathrm{4}}+{h}^{\mathrm{2}} }}\right\} \\ $$$$=\frac{\lambda}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} {h}}×\left\{\frac{{l}}{\:\sqrt{\frac{{l}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{3}{l}^{\mathrm{2}} }{\mathrm{4}}}}\right\} \\ $$$$=\frac{\lambda}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} {h}}×\mathrm{1} \\ $$$$=\frac{\frac{{q}}{{l}}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} \left(\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}{l}\right)}=\frac{{q}×\mathrm{2}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} ×\sqrt{\mathrm{3}}\:×{l}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{50}×\mathrm{10}^{−\mathrm{6}} ×\mathrm{9}×\mathrm{10}^{\mathrm{9}} ×\mathrm{2}}{\:\sqrt{\mathrm{3}}\:×\left(\mathrm{0}.\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{450}}{\:\sqrt{\mathrm{3}}}×\mathrm{2}×\mathrm{10}^{−\mathrm{6}+\mathrm{9}+\mathrm{2}} \\ $$$$=\mathrm{150}\sqrt{\mathrm{3}}\:×\mathrm{2}×\mathrm{10}^{\mathrm{5}} \\ $$$$=\mathrm{300}\sqrt{\mathrm{3}}\:×\mathrm{10}^{\mathrm{5}} \\ $$$$=\mathrm{3}\sqrt{\mathrm{3}}\:×\mathrm{10}^{\mathrm{7}} \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 08/Jun/18
see Q.37045
Commented by tanmay.chaudhury50@gmail.com last updated on 08/Jun/18
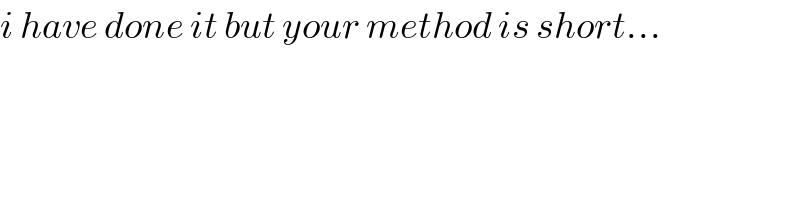
$${i}\:{have}\:{done}\:{it}\:{but}\:{your}\:{method}\:{is}\:{short}… \\ $$
Commented by Tinkutara last updated on 08/Jun/18
Thanks Sir!
Answered by ajfour last updated on 08/Jun/18
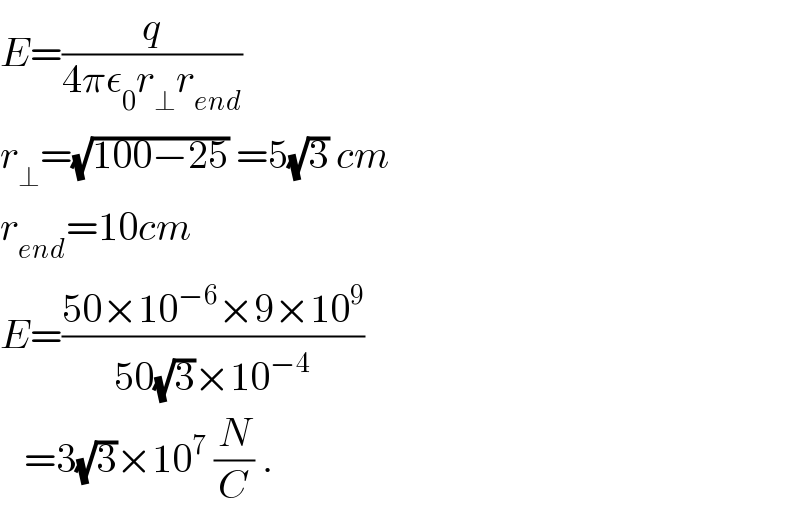
$${E}=\frac{{q}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {r}_{\bot} {r}_{{end}} } \\ $$$${r}_{\bot} =\sqrt{\mathrm{100}−\mathrm{25}}\:=\mathrm{5}\sqrt{\mathrm{3}}\:{cm} \\ $$$${r}_{{end}} =\mathrm{10}{cm} \\ $$$${E}=\frac{\mathrm{50}×\mathrm{10}^{−\mathrm{6}} ×\mathrm{9}×\mathrm{10}^{\mathrm{9}} }{\mathrm{50}\sqrt{\mathrm{3}}×\mathrm{10}^{−\mathrm{4}} } \\ $$$$\:\:\:=\mathrm{3}\sqrt{\mathrm{3}}×\mathrm{10}^{\mathrm{7}} \:\frac{{N}}{{C}}\:. \\ $$
Commented by Tinkutara last updated on 08/Jun/18
Thank you Sir.
