Question Number 69162 by Learner-123 last updated on 20/Sep/19
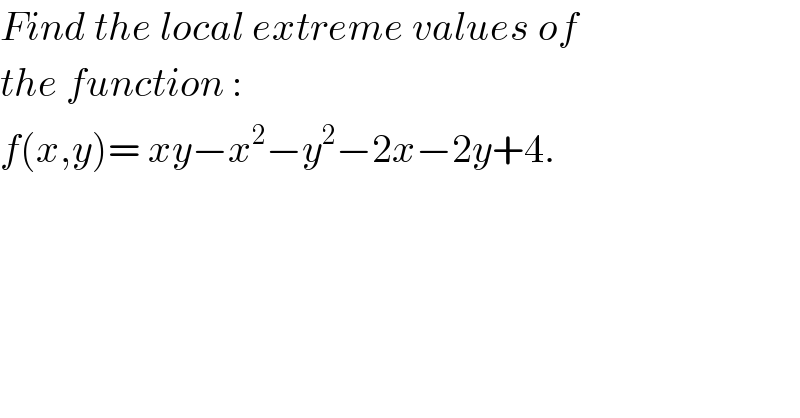
$${Find}\:{the}\:{local}\:{extreme}\:{values}\:{of} \\ $$$${the}\:{function}\:: \\ $$$${f}\left({x},{y}\right)=\:{xy}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{2}{y}+\mathrm{4}. \\ $$
Answered by MJS last updated on 20/Sep/19
![(d/dx)[−x^2 −y^2 +xy−2x−2y+4]=−2x+y−2 −2x+y−2=0 ⇒ x=((y−2)/2) f(((y−2)/2),y)=−(3/4)y^2 −3y+5 (d/dy)[−(3/4)y^2 −3y+5]=−(3/2)y−3 −(3/2)y−3=0 ⇒ y=−2 ⇒ x=−2 the 2^(nd) derivates are <0 ⇒ maximum at ((x),(y),((f(x, y))) ) = (((−2)),((−2)),(8) )](https://www.tinkutara.com/question/Q69164.png)
$$\frac{{d}}{{dx}}\left[−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{xy}−\mathrm{2}{x}−\mathrm{2}{y}+\mathrm{4}\right]=−\mathrm{2}{x}+{y}−\mathrm{2} \\ $$$$−\mathrm{2}{x}+{y}−\mathrm{2}=\mathrm{0}\:\Rightarrow\:{x}=\frac{{y}−\mathrm{2}}{\mathrm{2}} \\ $$$${f}\left(\frac{{y}−\mathrm{2}}{\mathrm{2}},{y}\right)=−\frac{\mathrm{3}}{\mathrm{4}}{y}^{\mathrm{2}} −\mathrm{3}{y}+\mathrm{5} \\ $$$$\frac{{d}}{{dy}}\left[−\frac{\mathrm{3}}{\mathrm{4}}{y}^{\mathrm{2}} −\mathrm{3}{y}+\mathrm{5}\right]=−\frac{\mathrm{3}}{\mathrm{2}}{y}−\mathrm{3} \\ $$$$−\frac{\mathrm{3}}{\mathrm{2}}{y}−\mathrm{3}=\mathrm{0}\:\Rightarrow\:{y}=−\mathrm{2}\:\Rightarrow\:{x}=−\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{derivates}\:\mathrm{are}\:<\mathrm{0}\:\Rightarrow\:\mathrm{maximum}\:\mathrm{at} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\\{{f}\left({x},\:{y}\right)}\end{pmatrix}\:=\begin{pmatrix}{−\mathrm{2}}\\{−\mathrm{2}}\\{\mathrm{8}}\end{pmatrix} \\ $$
Commented by Learner-123 last updated on 23/Sep/19

$${thanks}\:{sir}. \\ $$
