Question Number 168144 by cortano1 last updated on 04/Apr/22
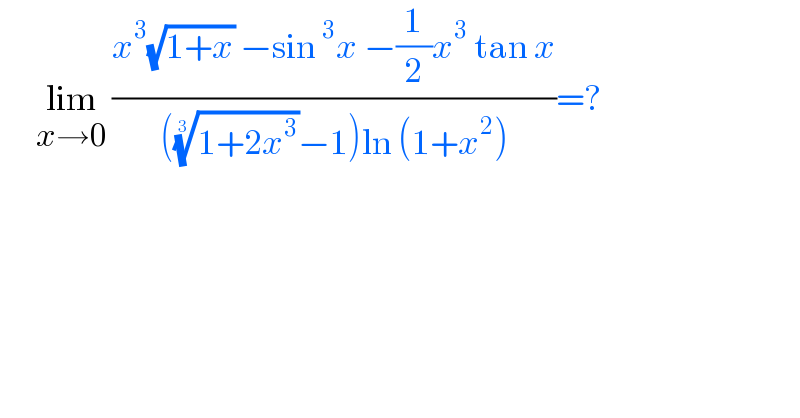
$$\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} \sqrt{\mathrm{1}+{x}}\:−\mathrm{sin}\:^{\mathrm{3}} {x}\:−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{3}} \:\mathrm{tan}\:{x}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{2}{x}^{\mathrm{3}} }−\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}=?\:\:\:\:\:\:\:\: \\ $$
Answered by qaz last updated on 05/Apr/22
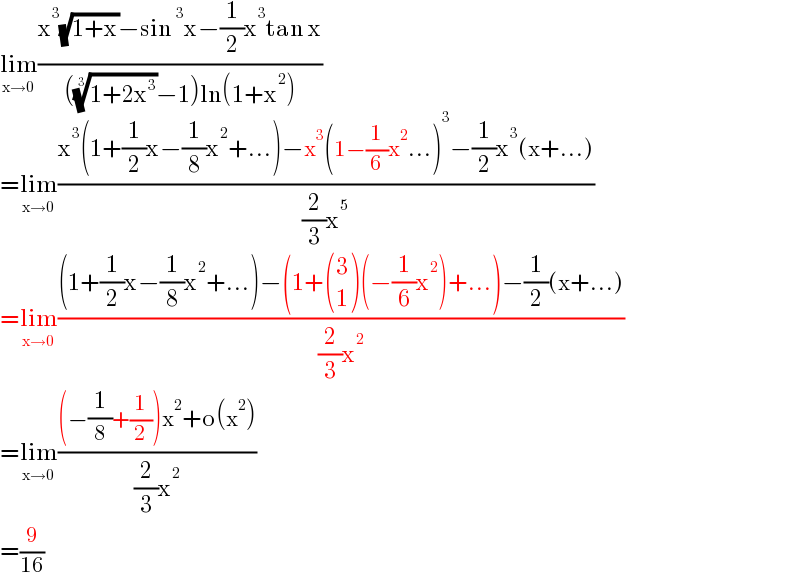
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{x}}−\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{3}} \mathrm{tan}\:\mathrm{x}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{2x}^{\mathrm{3}} }−\mathrm{1}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}^{\mathrm{2}} +…\right)−\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{2}} …\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}+…\right)}{\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{5}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}^{\mathrm{2}} +…\right)−\left(\mathrm{1}+\begin{pmatrix}{\mathrm{3}}\\{\mathrm{1}}\end{pmatrix}\left(−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{2}} \right)+…\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+…\right)}{\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}{\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{9}}{\mathrm{16}} \\ $$
Commented by cortano1 last updated on 05/Apr/22

$${ans}\:=\:\frac{\mathrm{9}}{\mathrm{16}} \\ $$
