Question-37089

Question Number 37089 by behi83417@gmail.com last updated on 08/Jun/18

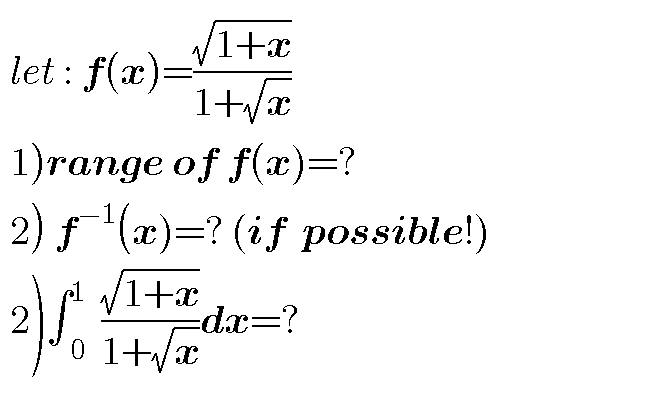
Commented by math khazana by abdo last updated on 09/Jun/18

1) f id defined on [0,+∞[ f^′ (x)= (((1/(2(√(1+x))))(1+(√x)) −(√(1+x))(1/(2(√x))))/((1+(√x))^2 )) = ((2(√x)(1+(√x))−2(1+x))/((1+(√x))^2 )) = ((2(√x) +2x −2−2x)/((1+(√x))^2 )) =((2((√x)−2))/((1+(√x))^2 )) if x≥4 f^′ ≥0 and f is increazing f([4,+∞[)=[f(4),f(+∞)[ =[((√5)/3) ,1[ if 0≤x≤4 f is decreasing so f ([0,4])=[f(4),f(0)] =[((√5)/3),1]

$$\left.\mathrm{1}\right)\:{f}\:{id}\:{defined}\:{on}\:\left[\mathrm{0},+\infty\left[\right.\right. \\ $$$${f}^{'} \left({x}\right)=\:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}\left(\mathrm{1}+\sqrt{{x}}\right)\:−\sqrt{\mathrm{1}+{x}}\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\left(\mathrm{1}+\sqrt{{x}}\right)^{\mathrm{2}} } \\ $$$$=\:\:\frac{\mathrm{2}\sqrt{{x}}\left(\mathrm{1}+\sqrt{{x}}\right)−\mathrm{2}\left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}+\sqrt{{x}}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{2}\sqrt{{x}}\:+\mathrm{2}{x}\:−\mathrm{2}−\mathrm{2}{x}}{\left(\mathrm{1}+\sqrt{{x}}\right)^{\mathrm{2}} } \\ $$$$\:=\frac{\mathrm{2}\left(\sqrt{{x}}−\mathrm{2}\right)}{\left(\mathrm{1}+\sqrt{{x}}\right)^{\mathrm{2}} }\:\:{if}\:{x}\geqslant\mathrm{4}\:\:{f}^{'} \geqslant\mathrm{0}\:\:{and}\:{f}\:{is}\:{increazing} \\ $$$${f}\left(\left[\mathrm{4},+\infty\left[\right)=\left[{f}\left(\mathrm{4}\right),{f}\left(+\infty\right)\left[\:=\left[\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\:,\mathrm{1}\left[\right.\right.\right.\right.\right.\right. \\ $$$${if}\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{4}\:\:{f}\:{is}\:{decreasing}\:{so} \\ $$$${f}\:\left(\left[\mathrm{0},\mathrm{4}\right]\right)=\left[{f}\left(\mathrm{4}\right),{f}\left(\mathrm{0}\right)\right]\:=\left[\frac{\sqrt{\mathrm{5}}}{\mathrm{3}},\mathrm{1}\right] \\ $$

Commented by math khazana by abdo last updated on 09/Jun/18

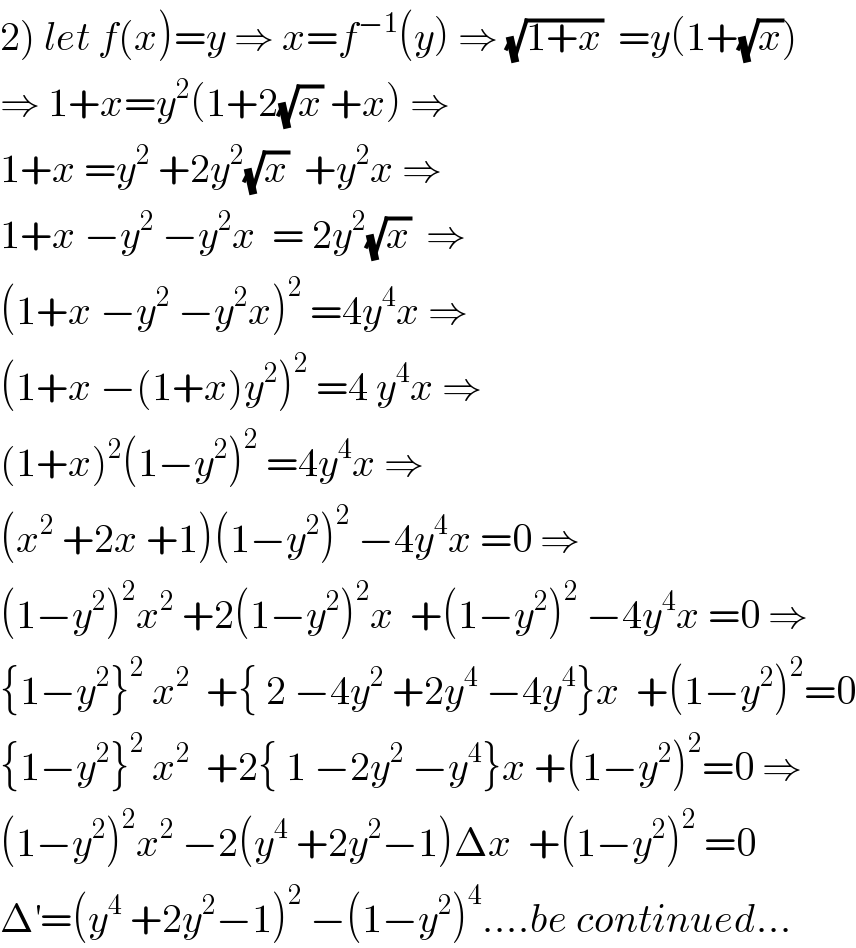
2) let f(x)=y ⇒ x=f^(−1) (y) ⇒ (√(1+x)) =y(1+(√x)) ⇒ 1+x=y^2 (1+2(√x) +x) ⇒ 1+x =y^2 +2y^2 (√x) +y^2 x ⇒ 1+x −y^2 −y^2 x = 2y^2 (√x) ⇒ (1+x −y^2 −y^2 x)^2 =4y^4 x ⇒ (1+x −(1+x)y^2 )^2 =4 y^4 x ⇒ (1+x)^2 (1−y^2 )^2 =4y^4 x ⇒ (x^2 +2x +1)(1−y^2 )^2 −4y^4 x =0 ⇒ (1−y^2 )^2 x^2 +2(1−y^2 )^2 x +(1−y^2 )^2 −4y^4 x =0 ⇒ {1−y^2 }^2 x^2 +{ 2 −4y^2 +2y^4 −4y^4 }x +(1−y^2 )^2 =0 {1−y^2 }^2 x^2 +2{ 1 −2y^2 −y^4 }x +(1−y^2 )^2 =0 ⇒ (1−y^2 )^2 x^2 −2(y^4 +2y^2 −1)Δx +(1−y^2 )^2 =0 Δ^′ =(y^4 +2y^2 −1)^2 −(1−y^2 )^4 ....be continued...

$$\left.\mathrm{2}\right)\:{let}\:{f}\left({x}\right)={y}\:\Rightarrow\:{x}={f}^{−\mathrm{1}} \left({y}\right)\:\Rightarrow\:\sqrt{\mathrm{1}+{x}}\:\:={y}\left(\mathrm{1}+\sqrt{{x}}\right) \\ $$$$\Rightarrow\:\mathrm{1}+{x}={y}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{2}\sqrt{{x}}\:+{x}\right)\:\Rightarrow \\ $$$$\mathrm{1}+{x}\:={y}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} \sqrt{{x}}\:\:+{y}^{\mathrm{2}} {x}\:\Rightarrow \\ $$$$\mathrm{1}+{x}\:−{y}^{\mathrm{2}} \:−{y}^{\mathrm{2}} {x}\:\:=\:\mathrm{2}{y}^{\mathrm{2}} \sqrt{{x}}\:\:\Rightarrow \\ $$$$\left(\mathrm{1}+{x}\:−{y}^{\mathrm{2}} \:−{y}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:=\mathrm{4}{y}^{\mathrm{4}} {x}\:\Rightarrow \\ $$$$\left(\mathrm{1}+{x}\:−\left(\mathrm{1}+{x}\right){y}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\mathrm{4}\:{y}^{\mathrm{4}} {x}\:\Rightarrow \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\mathrm{4}{y}^{\mathrm{4}} {x}\:\Rightarrow \\ $$$$\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{1}\right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} \:−\mathrm{4}{y}^{\mathrm{4}} {x}\:=\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} {x}^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} {x}\:\:+\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} \:−\mathrm{4}{y}^{\mathrm{4}} {x}\:=\mathrm{0}\:\Rightarrow \\ $$$$\left\{\mathrm{1}−{y}^{\mathrm{2}} \right\}^{\mathrm{2}} \:{x}^{\mathrm{2}} \:\:+\left\{\:\mathrm{2}\:−\mathrm{4}{y}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{4}} \:−\mathrm{4}{y}^{\mathrm{4}} \right\}{x}\:\:+\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left\{\mathrm{1}−{y}^{\mathrm{2}} \right\}^{\mathrm{2}} \:{x}^{\mathrm{2}} \:\:+\mathrm{2}\left\{\:\mathrm{1}\:−\mathrm{2}{y}^{\mathrm{2}} \:−{y}^{\mathrm{4}} \right\}{x}\:+\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} {x}^{\mathrm{2}} \:−\mathrm{2}\left({y}^{\mathrm{4}} \:+\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}\right)\Delta{x}\:\:+\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\mathrm{0} \\ $$$$\Delta^{'} =\left({y}^{\mathrm{4}} \:+\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \:−\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{4}} ….{be}\:{continued}… \\ $$

Commented by math khazana by abdo last updated on 09/Jun/18

3) let I = ∫_0 ^1 ((√(1+x))/(1+(√x))) dx changement (√x)=t give I = ∫_0 ^1 ((√(1+t^2 ))/(1+t)) 2t dt =2 ∫_0 ^1 (t/(1+t))(√(1+t^2 )) dt =2{ ∫_0 ^1 (√(1+t^2 )) dt −∫_0 ^1 ((√(1+t^2 ))/(1+t))dt } ∫_0 ^1 (√(1+t^2 )) dt =_(t=sh(u)) ∫_o ^(ln(1+(√2))) ch(u)ch(u)du =(1/2) ∫_0 ^(ln(1+(√2))) (1+ch(2u))du =(1/2)ln(1+(√2)) +(1/4) [sh(2u)]_0 ^(ln(1+(√2))) but sh(2u) =((e^(2u) +e^(−2u) )/2) ⇒ sh(2ln(1+(√2)) = (((1+(√2))^2 +(1+(√2))^(−2) )/2) ⇒ ∫_0 ^1 (√(1+t^2 ))dt = (1/2)ln(1+(√2)) +(1/8){ (1+(√2))^2 +(1+(√2))^(−2) } letfind ∫_0 ^1 ((√(1+t^2 ))/(1+t)) dt chang. t=sh(x) give ∫_0 ^1 ((√(1+t^2 ))/(1+t)) dt= ∫_0 ^(ln(1+(√2))) ((ch(x))/(1+sh(x))) ch(x)dx = ∫_0 ^(ln(1+(√2))) (1/(1+sh(x))) ((1+ch(2x))/2) dx =(1/2) ∫_0 ^(ln(1+(√2))) ((1 +((e^(2x) +e^(−2x) )/2))/(1+ ((e^x +e^(−x) )/2))) dx =(1/2) ∫_0 ^(ln(1+(√2))) ((2 +e^(2x) +e^(−2x) )/(2+e^x +e^(−x) )) dx =_(e^x =t) (1/2) ∫_1 ^(1+(√2)) ((2 +t^(2 ) +(1/t^2 ))/(2 +t +(1/t))) dt =(1/2) ∫_1 ^(1+(√2)) ((2t^2 +t^4 +1)/(2t +t^2 +1)) (1/t) dt =(1/2) ∫_1 ^(1 +(√2)) ((t^4 +2t^2 +1)/(t^3 +2t^2 +t)) dt =(1/2) ∫_1 ^(1 +(√2)) ((t(t^3 +2t^2 +t) −2t^3 +t^2 +2t^2 +1)/(t^3 +2t^2 +t)) dt =(1/2) ∫_1 ^(1+(√2)) t dt +(1/2) ∫_1 ^(1+(√2)) ((−2t^3 +3t^2 +1)/(t^3 +2t^2 +t))dt =(1/4){ (1+(√2))^2 −1} +(1/2) ∫_1 ^(1+(√2)) ((−2(t^3 +2t^2 +t)+4t^2 +2t +3t^(2 ) +1)/(t^3 +2t^2 +t)) =(1/4){2−2(√2)) −1((√2)) +(1/2)∫_1 ^(1+(√2)) ((7t^2 +2t +1)/(t(t^2 +2t +1)))dt let decompose F(t) = ((7t^2 +2t +1)/(t(t+1)^2 )) F(t) = (a/t) +(b/(t+1)) +(c/((t+1)^2 )) ....be continued...

$$\left.\mathrm{3}\right)\:{let}\:{I}\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\sqrt{\mathrm{1}+{x}}}{\mathrm{1}+\sqrt{{x}}}\:{dx}\:{changement}\:\sqrt{{x}}={t}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+{t}}\:\mathrm{2}{t}\:{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}}{\mathrm{1}+{t}}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\:{dt}\:=\mathrm{2}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+{t}}{dt}\:\right\} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:=_{{t}={sh}\left({u}\right)} \:\:\int_{{o}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:{ch}\left({u}\right){ch}\left({u}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\left(\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\:+\frac{\mathrm{1}}{\mathrm{4}}\:\left[{sh}\left(\mathrm{2}{u}\right)\right]_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:{but} \\ $$$${sh}\left(\mathrm{2}{u}\right)\:=\frac{{e}^{\mathrm{2}{u}} \:+{e}^{−\mathrm{2}{u}} }{\mathrm{2}}\:\Rightarrow\:{sh}\left(\mathrm{2}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right. \\ $$$$=\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:\:+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{2}} \right\} \\ $$$${letfind}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+{t}}\:{dt}\:\:{chang}.\:{t}={sh}\left({x}\right)\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+{t}}\:{dt}=\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\frac{{ch}\left({x}\right)}{\mathrm{1}+{sh}\left({x}\right)}\:{ch}\left({x}\right){dx} \\ $$$$=\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{sh}\left({x}\right)}\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\:\frac{\mathrm{1}\:+\frac{{e}^{\mathrm{2}{x}} \:+{e}^{−\mathrm{2}{x}} }{\mathrm{2}}}{\mathrm{1}+\:\frac{{e}^{{x}} \:+{e}^{−{x}} }{\mathrm{2}}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\frac{\mathrm{2}\:+{e}^{\mathrm{2}{x}} \:+{e}^{−\mathrm{2}{x}} }{\mathrm{2}+{e}^{{x}} \:+{e}^{−{x}} }\:{dx} \\ $$$$=_{{e}^{{x}} \:={t}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:\:\:\frac{\mathrm{2}\:\:+{t}^{\mathrm{2}\:} \:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\mathrm{2}\:+{t}\:+\frac{\mathrm{1}}{{t}}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} \:+{t}^{\mathrm{4}} \:+\mathrm{1}}{\mathrm{2}{t}\:+{t}^{\mathrm{2}} \:+\mathrm{1}}\:\frac{\mathrm{1}}{{t}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{1}\:+\sqrt{\mathrm{2}}} \:\:\frac{{t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+{t}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{1}\:+\sqrt{\mathrm{2}}} \:\:\:\frac{{t}\left({t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+{t}\right)\:−\mathrm{2}{t}^{\mathrm{3}} \:+{t}^{\mathrm{2}} \:\:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+{t}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:{t}\:{dt}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\frac{−\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}\right\}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \frac{−\mathrm{2}\left({t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+{t}\right)+\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{3}{t}^{\mathrm{2}\:} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\right)\:\:−\mathrm{1}\left(\sqrt{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:\frac{\mathrm{7}{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{1}\right)}{dt} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\:\frac{\mathrm{7}{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{1}}{{t}\left({t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left({t}\right)\:=\:\frac{{a}}{{t}}\:+\frac{{b}}{{t}+\mathrm{1}}\:+\frac{{c}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:\:….{be}\:{continued}… \\ $$

Commented by behi83417@gmail.com last updated on 09/Jun/18

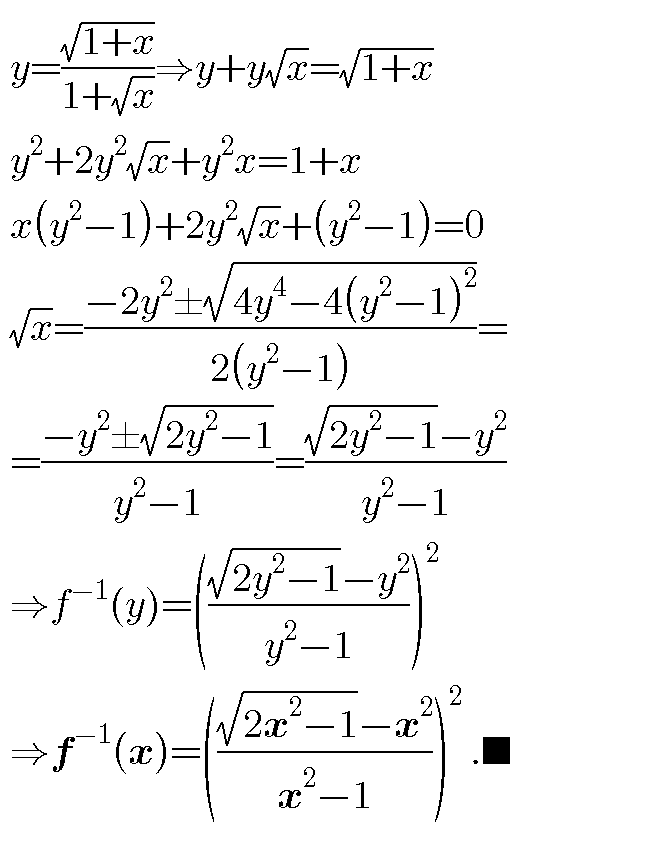
Commented by prakash jain last updated on 09/Jun/18

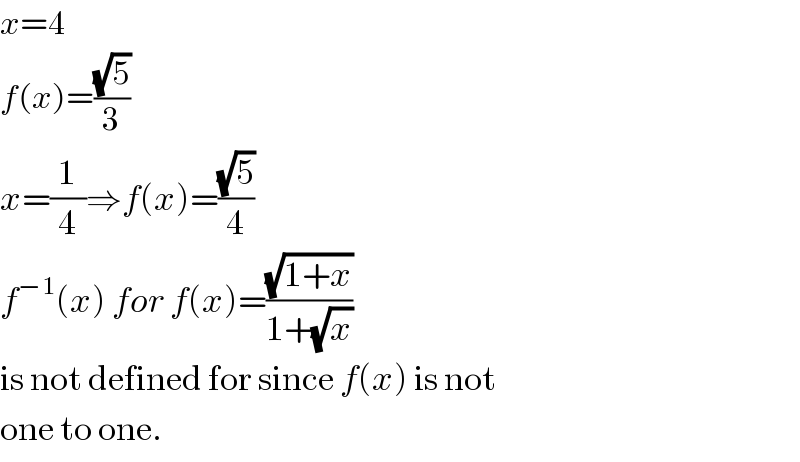
x=4 f(x)=((√5)/3) x=(1/4)⇒f(x)=((√5)/4) f^(−1) (x) for f(x)=((√(1+x))/(1+(√x))) is not defined for since f(x) is not one to one.

$${x}=\mathrm{4} \\ $$$${f}\left({x}\right)=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow{f}\left({x}\right)=\frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:{for}\:{f}\left({x}\right)=\frac{\sqrt{\mathrm{1}+{x}}}{\mathrm{1}+\sqrt{{x}}}\: \\ $$$$\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:\mathrm{since}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{one}\:\mathrm{to}\:\mathrm{one}. \\ $$

Commented by behi83417@gmail.com last updated on 09/Jun/18

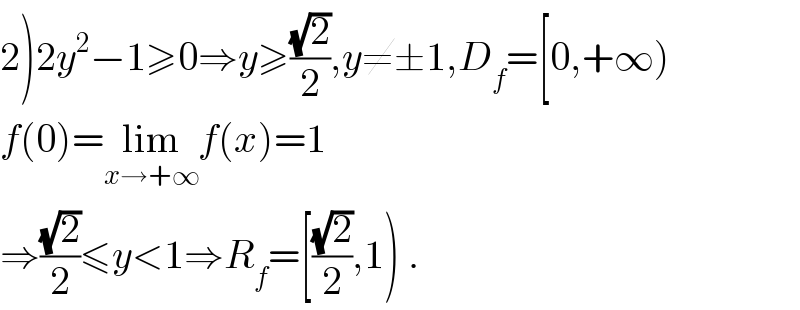
2)2y^2 −1≥0⇒y≥((√2)/2),y≠±1,D_f =[0,+∞) f(0)=lim_(x→+∞) f(x)=1 ⇒((√2)/2)≤y<1⇒R_f =[((√2)/2),1) .

$$\left.\mathrm{2}\right)\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}\geqslant\mathrm{0}\Rightarrow{y}\geqslant\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},{y}\neq\pm\mathrm{1},{D}_{{f}} =\left[\mathrm{0},+\infty\right) \\ $$$${f}\left(\mathrm{0}\right)=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant{y}<\mathrm{1}\Rightarrow{R}_{{f}} =\left[\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\mathrm{1}\right)\:. \\ $$

Commented by prakash jain last updated on 09/Jun/18

f(x)=((√5)/3) what is f^(−1) (x)? f((1/4)) and f(4) both give f(x)=((√5)/3) so f^(−1) (x) is multivalued and hence f^(−1) (x) not a function by definition.

$${f}\left({x}\right)=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\:\mathrm{what}\:\mathrm{is}\:{f}^{−\mathrm{1}} \left({x}\right)? \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:\mathrm{and}\:{f}\left(\mathrm{4}\right)\:\mathrm{both}\:\mathrm{give} \\ $$$${f}\left({x}\right)=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\:\mathrm{so}\:{f}^{−\mathrm{1}} \left({x}\right)\:\mathrm{is}\:\mathrm{multivalued} \\ $$$$\mathrm{and}\:\mathrm{hence}\:{f}^{−\mathrm{1}} \left({x}\right)\:\mathrm{not}\:\mathrm{a}\:\mathrm{function}\:\mathrm{by}\:\mathrm{definition}. \\ $$

Commented by math khazana by abdo last updated on 09/Jun/18

$${hello}\:{sir}\:{prakash}\:\:{why}\:{are}\:{you}\:\:{absent}\:{from}\:{this} \\ $$$${platform}… \\ $$

Commented by prakash jain last updated on 10/Jun/18

I am not completely absent. I read messages daily. My office work load is high and I am not getting time to work problems.

$$\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{completely}\:\mathrm{absent}.\:\mathrm{I}\:\mathrm{read} \\ $$$$\mathrm{messages}\:\mathrm{daily}. \\ $$$$ \\ $$$$\mathrm{My}\:\mathrm{office}\:\mathrm{work}\:\mathrm{load}\:\mathrm{is}\:\mathrm{high}\:\mathrm{and}\:\mathrm{I} \\ $$$$\mathrm{am}\:\mathrm{not}\:\mathrm{getting}\:\mathrm{time}\:\mathrm{to}\:\mathrm{work}\: \\ $$$$\mathrm{problems}. \\ $$

Commented by math khazana by abdo last updated on 10/Jun/18

$${nevermind}\:{sir}\:.. \\ $$

Answered by ajfour last updated on 09/Jun/18

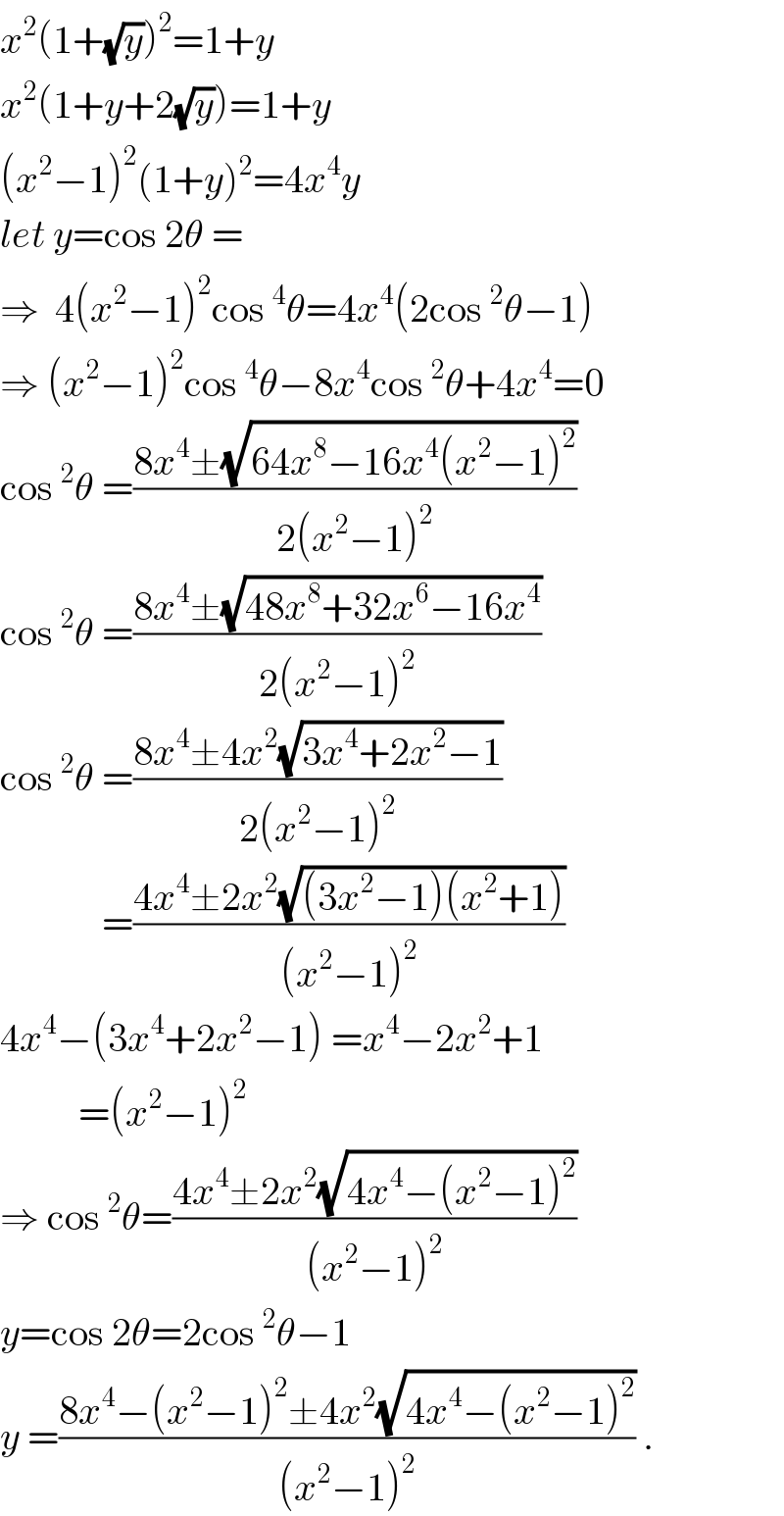
x^2 (1+(√y))^2 =1+y x^2 (1+y+2(√y))=1+y (x^2 −1)^2 (1+y)^2 =4x^4 y let y=cos 2θ = ⇒ 4(x^2 −1)^2 cos^4 θ=4x^4 (2cos^2 θ−1) ⇒ (x^2 −1)^2 cos^4 θ−8x^4 cos^2 θ+4x^4 =0 cos^2 θ =((8x^4 ±(√(64x^8 −16x^4 (x^2 −1)^2 )))/(2(x^2 −1)^2 )) cos^2 θ =((8x^4 ±(√(48x^8 +32x^6 −16x^4 )))/(2(x^2 −1)^2 )) cos^2 θ =((8x^4 ±4x^2 (√(3x^4 +2x^2 −1)))/(2(x^2 −1)^2 )) =((4x^4 ±2x^2 (√((3x^2 −1)(x^2 +1))))/((x^2 −1)^2 )) 4x^4 −(3x^4 +2x^2 −1) =x^4 −2x^2 +1 =(x^2 −1)^2 ⇒ cos^2 θ=((4x^4 ±2x^2 (√(4x^4 −(x^2 −1)^2 )))/((x^2 −1)^2 )) y=cos 2θ=2cos^2 θ−1 y =((8x^4 −(x^2 −1)^2 ±4x^2 (√(4x^4 −(x^2 −1)^2 )))/((x^2 −1)^2 )) .

$${x}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{{y}}\right)^{\mathrm{2}} =\mathrm{1}+{y} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}+{y}+\mathrm{2}\sqrt{{y}}\right)=\mathrm{1}+{y} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}+{y}\right)^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{4}} {y} \\ $$$${let}\:{y}=\mathrm{cos}\:\mathrm{2}\theta\:= \\ $$$$\Rightarrow\:\:\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{4}} \theta=\mathrm{4}{x}^{\mathrm{4}} \left(\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1}\right) \\ $$$$\Rightarrow\:\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{4}} \theta−\mathrm{8}{x}^{\mathrm{4}} \mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{4}{x}^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \theta\:=\frac{\mathrm{8}{x}^{\mathrm{4}} \pm\sqrt{\mathrm{64}{x}^{\mathrm{8}} −\mathrm{16}{x}^{\mathrm{4}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \theta\:=\frac{\mathrm{8}{x}^{\mathrm{4}} \pm\sqrt{\mathrm{48}{x}^{\mathrm{8}} +\mathrm{32}{x}^{\mathrm{6}} −\mathrm{16}{x}^{\mathrm{4}} }}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \theta\:=\frac{\mathrm{8}{x}^{\mathrm{4}} \pm\mathrm{4}{x}^{\mathrm{2}} \sqrt{\mathrm{3}{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}{x}^{\mathrm{4}} \pm\mathrm{2}{x}^{\mathrm{2}} \sqrt{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{4}{x}^{\mathrm{4}} −\left(\mathrm{3}{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)\:={x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{cos}\:^{\mathrm{2}} \theta=\frac{\mathrm{4}{x}^{\mathrm{4}} \pm\mathrm{2}{x}^{\mathrm{2}} \sqrt{\mathrm{4}{x}^{\mathrm{4}} −\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${y}=\mathrm{cos}\:\mathrm{2}\theta=\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1} \\ $$$${y}\:=\frac{\mathrm{8}{x}^{\mathrm{4}} −\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \pm\mathrm{4}{x}^{\mathrm{2}} \sqrt{\mathrm{4}{x}^{\mathrm{4}} −\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply