Question Number 37108 by rahul 19 last updated on 09/Jun/18
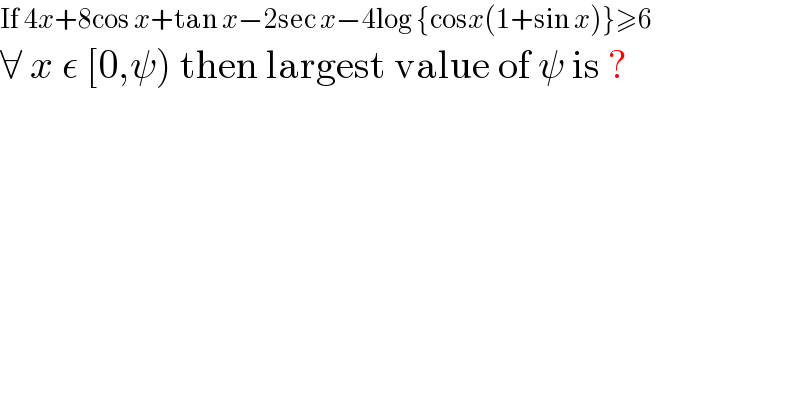
$$\mathrm{If}\:\mathrm{4}{x}+\mathrm{8cos}\:{x}+\mathrm{tan}\:{x}−\mathrm{2sec}\:{x}−\mathrm{4log}\:\left\{\mathrm{cos}{x}\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\right\}\geqslant\mathrm{6} \\ $$$$\forall\:{x}\:\epsilon\:\left[\mathrm{0},\psi\right)\:\mathrm{then}\:\mathrm{largest}\:\mathrm{value}\:\mathrm{of}\:\psi\:\mathrm{is}\:? \\ $$
Answered by ajfour last updated on 09/Jun/18
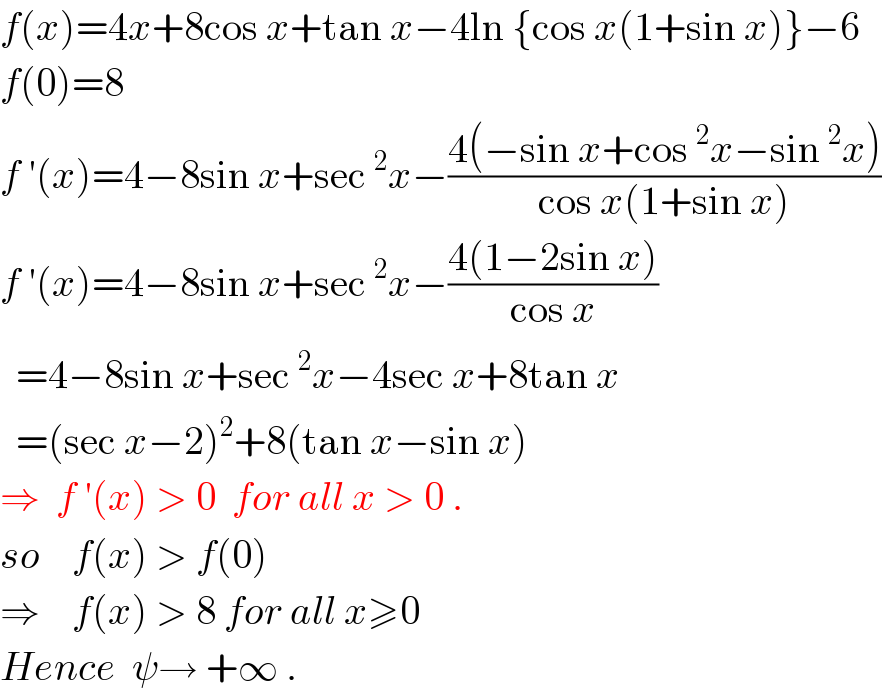
$${f}\left({x}\right)=\mathrm{4}{x}+\mathrm{8cos}\:{x}+\mathrm{tan}\:{x}−\mathrm{4ln}\:\left\{\mathrm{cos}\:{x}\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\right\}−\mathrm{6} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{8} \\ $$$${f}\:'\left({x}\right)=\mathrm{4}−\mathrm{8sin}\:{x}+\mathrm{sec}\:^{\mathrm{2}} {x}−\frac{\mathrm{4}\left(−\mathrm{sin}\:{x}+\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)}{\mathrm{cos}\:{x}\left(\mathrm{1}+\mathrm{sin}\:{x}\right)} \\ $$$${f}\:'\left({x}\right)=\mathrm{4}−\mathrm{8sin}\:{x}+\mathrm{sec}\:^{\mathrm{2}} {x}−\frac{\mathrm{4}\left(\mathrm{1}−\mathrm{2sin}\:{x}\right)}{\mathrm{cos}\:{x}} \\ $$$$\:\:=\mathrm{4}−\mathrm{8sin}\:{x}+\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{4sec}\:{x}+\mathrm{8tan}\:{x} \\ $$$$\:\:=\left(\mathrm{sec}\:{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{8}\left(\mathrm{tan}\:{x}−\mathrm{sin}\:{x}\right)\: \\ $$$$\Rightarrow\:\:{f}\:'\left({x}\right)\:>\:\mathrm{0}\:\:{for}\:{all}\:{x}\:>\:\mathrm{0}\:. \\ $$$${so}\:\:\:\:{f}\left({x}\right)\:>\:{f}\left(\mathrm{0}\right)\: \\ $$$$\Rightarrow\:\:\:\:{f}\left({x}\right)\:>\:\mathrm{8}\:{for}\:{all}\:{x}\geqslant\mathrm{0} \\ $$$${Hence}\:\:\psi\rightarrow\:+\infty\:. \\ $$
