Question Number 37235 by abdo.msup.com last updated on 11/Jun/18
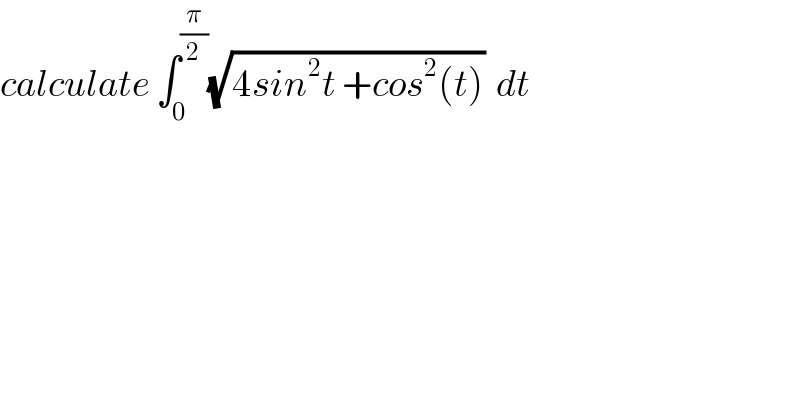
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{4}{sin}^{\mathrm{2}} {t}\:+{cos}^{\mathrm{2}} \left({t}\right)}\:\:{dt} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Jun/18
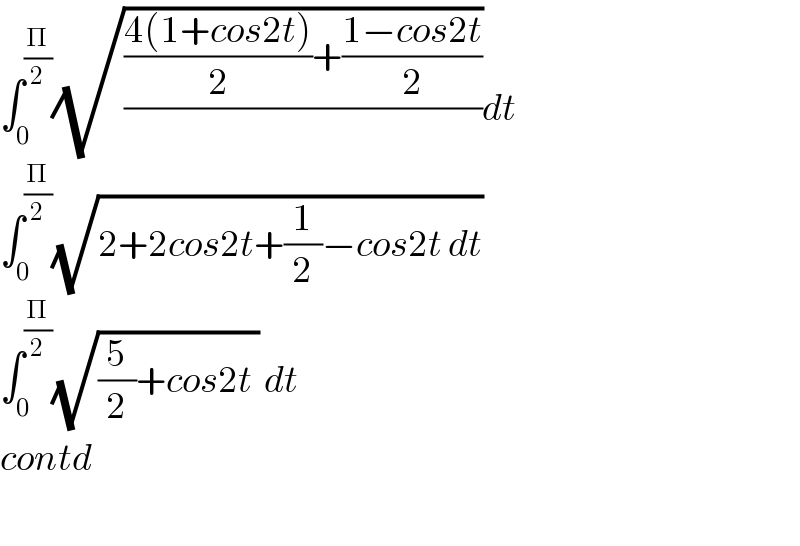
$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \sqrt{\frac{\frac{\mathrm{4}\left(\mathrm{1}+{cos}\mathrm{2}{t}\right)}{\mathrm{2}}+\frac{\mathrm{1}−{cos}\mathrm{2}{t}}{\mathrm{2}}}{}}{dt} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \sqrt{\mathrm{2}+\mathrm{2}{cos}\mathrm{2}{t}+\frac{\mathrm{1}}{\mathrm{2}}−{cos}\mathrm{2}{t}\:{dt}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{5}}{\mathrm{2}}+{cos}\mathrm{2}{t}\:}\:{dt} \\ $$$${contd} \\ $$$$ \\ $$
