Question Number 69183 by Tony Lin last updated on 21/Sep/19

Commented by Tony Lin last updated on 21/Sep/19
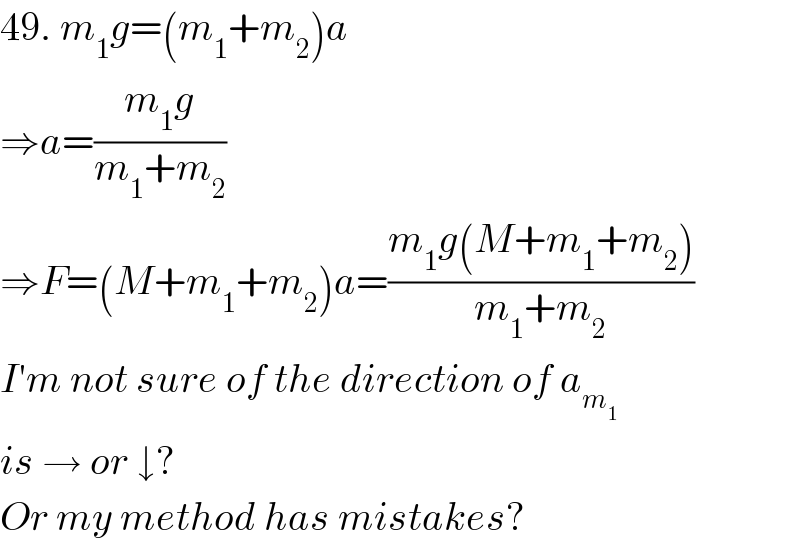
$$\mathrm{49}.\:{m}_{\mathrm{1}} {g}=\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right){a} \\ $$$$\Rightarrow{a}=\frac{{m}_{\mathrm{1}} {g}}{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} } \\ $$$$\Rightarrow{F}=\left({M}+{m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right){a}=\frac{{m}_{\mathrm{1}} {g}\left({M}+{m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right)}{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} } \\ $$$${I}'{m}\:{not}\:{sure}\:{of}\:{the}\:{direction}\:{of}\:{a}_{{m}_{\mathrm{1}} } \\ $$$${is}\:\rightarrow\:{or}\:\downarrow? \\ $$$${Or}\:{my}\:{method}\:{has}\:{mistakes}? \\ $$
Commented by Tony Lin last updated on 21/Sep/19

$$\mathrm{53}.\:{Does}\:{this}\:{example}\:{satisfies}\:{the}\: \\ $$$${conservation}\:{of}\:{horizontal}\:{momentum}? \\ $$$${If}\:{Yes},{how}\:{to}\:{solve}\:{it}? \\ $$
Answered by mr W last updated on 21/Sep/19
Commented by mr W last updated on 21/Sep/19

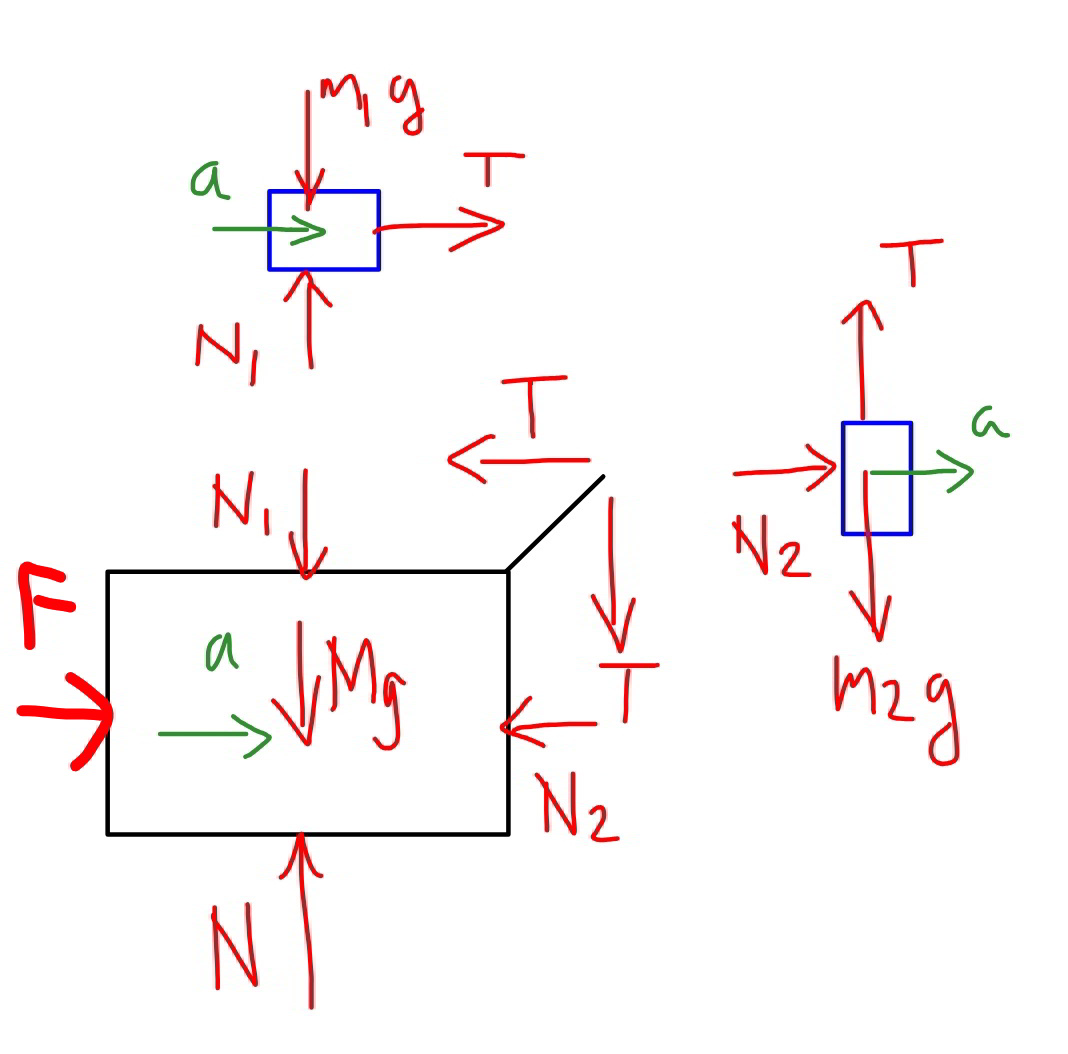
$$\left({note}:\:{in}\:{my}\:{solution}\:{m}_{\mathrm{1}} \:{corresponds}\right. \\ $$$${with}\:{m}_{\mathrm{2}} \:{in}\:{the}\:{question}\:{and}\:{m}_{\mathrm{2}} \:{with} \\ $$$$\left.{m}_{\mathrm{1}} \right) \\ $$$$ \\ $$$${all}\:{blocks}\:{must}\:{have}\:{the}\:{same}\:{horizontal} \\ $$$${motion}\:{and}\:{no}\:{vertical}\:{motion}. \\ $$$$ \\ $$$${T}={m}_{\mathrm{2}} {g} \\ $$$${N}_{\mathrm{2}} ={m}_{\mathrm{2}} {a} \\ $$$${N}_{\mathrm{1}} ={m}_{\mathrm{1}} {g} \\ $$$${T}={m}_{\mathrm{1}} {a}={m}_{\mathrm{2}} {g} \\ $$$$\Rightarrow{a}=\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }{g} \\ $$$${F}−{N}_{\mathrm{2}} −{T}={Ma} \\ $$$$\Rightarrow{F}={Ma}+{N}_{\mathrm{2}} +{T}={Ma}+{m}_{\mathrm{2}} {a}+{m}_{\mathrm{1}} {a} \\ $$$$\Rightarrow{F}=\left({M}+{m}_{\mathrm{2}} +{m}_{\mathrm{1}} \right){a}=\frac{\left({M}+{m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right){m}_{\mathrm{2}} {g}}{{m}_{\mathrm{1}} } \\ $$
Commented by Tony Lin last updated on 21/Sep/19

$${Thanks},{I}\:{got}\:{it}. \\ $$
