Menu Close

I-2-0-1-2-sin-1-x-x-dx-0-1-tan-1-x-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 102790 by bobhans last updated on 11/Jul/20
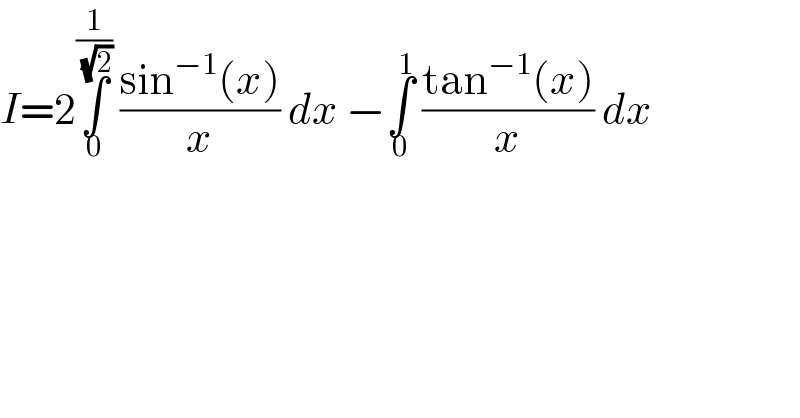
I=2∫_0 ^(1/( (√2))) ((sin^(−1) (x))/x) dx −∫_0 ^1 ((tan^(−1) (x))/x) dx
$${I}=\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} {\int}}\:\frac{\mathrm{sin}^{−\mathrm{1}} \left({x}\right)}{{x}}\:{dx}\:−\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{{x}}\:{dx}\: \\ $$
Answered by bramlex last updated on 11/Jul/20
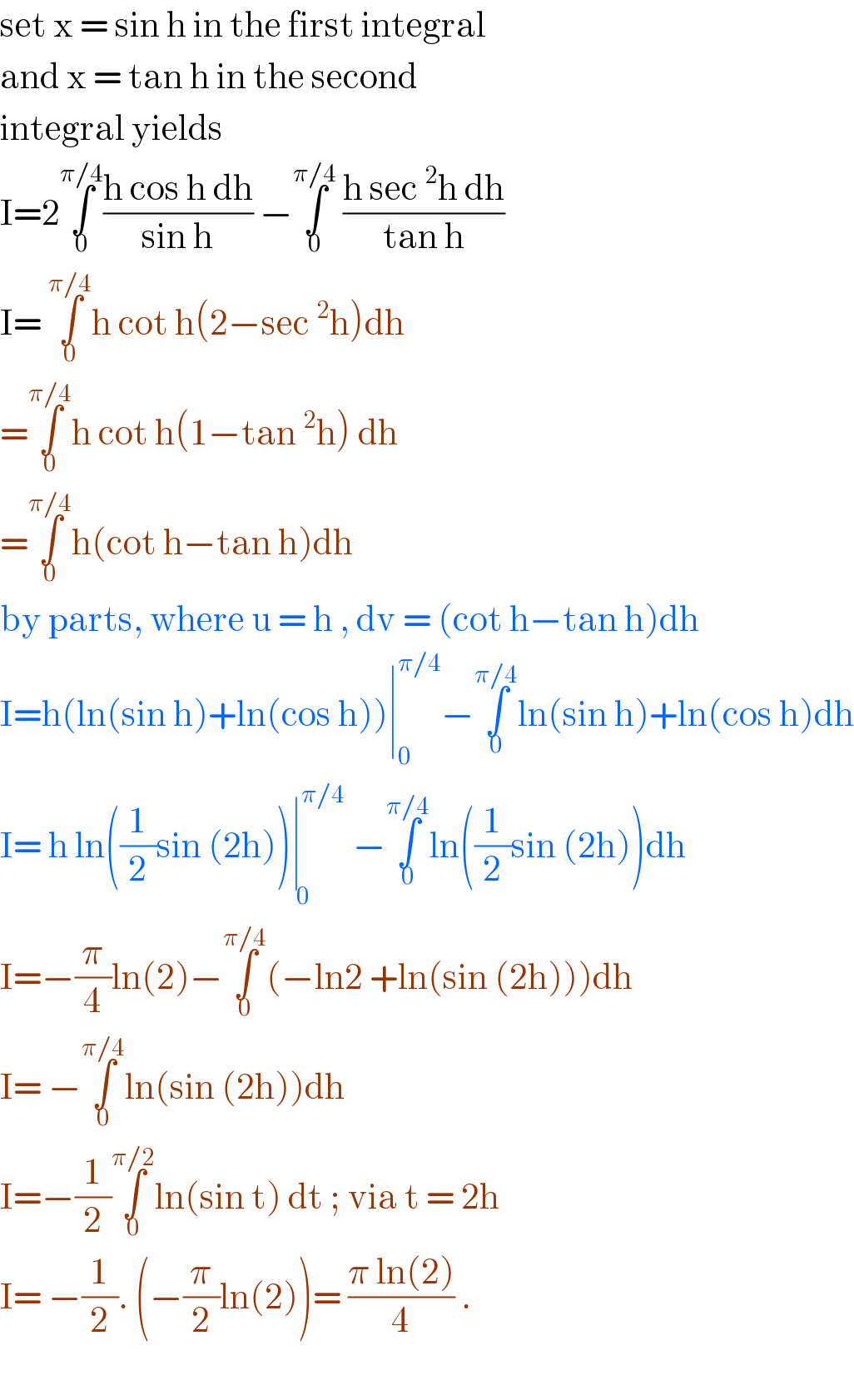
set x = sin h in the first integral and x = tan h in the second integral yields I=2∫_0 ^(π/4) ((h cos h dh)/(sin h)) −∫_0 ^(π/4) ((h sec^2 h dh)/(tan h)) I= ∫_0 ^(π/4) h cot h(2−sec^2 h)dh =∫_0 ^(π/4) h cot h(1−tan^2 h) dh =∫_0 ^(π/4) h(cot h−tan h)dh by parts, where u = h , dv = (cot h−tan h)dh I=h(ln(sin h)+ln(cos h))∣_0 ^(π/4) −∫_0 ^(π/4) ln(sin h)+ln(cos h)dh I= h ln((1/2)sin (2h))∣^(π/4) _( 0) −∫_0 ^(π/4) ln((1/2)sin (2h))dh I=−(π/4)ln(2)−∫_0 ^(π/4) (−ln2 +ln(sin (2h)))dh I= −∫_0 ^(π/4) ln(sin (2h))dh I=−(1/2)∫_0 ^(π/2) ln(sin t) dt ; via t = 2h I= −(1/2). (−(π/2)ln(2))= ((π ln(2))/4) .
$$\mathrm{set}\:\mathrm{x}\:=\:\mathrm{sin}\:\mathrm{h}\:\mathrm{in}\:\mathrm{the}\:\mathrm{first}\:\mathrm{integral} \\ $$$$\mathrm{and}\:\mathrm{x}\:=\:\mathrm{tan}\:\mathrm{h}\:\mathrm{in}\:\mathrm{the}\:\mathrm{second} \\ $$$$\mathrm{integral}\:\mathrm{yields}\: \\ $$$$\mathrm{I}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{\mathrm{h}\:\mathrm{cos}\:\mathrm{h}\:\mathrm{dh}}{\mathrm{sin}\:\mathrm{h}}\:−\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\mathrm{h}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{h}\:\mathrm{dh}}{\mathrm{tan}\:\mathrm{h}} \\ $$$$\mathrm{I}=\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\mathrm{h}\:\mathrm{cot}\:\mathrm{h}\left(\mathrm{2}−\mathrm{sec}\:^{\mathrm{2}} \mathrm{h}\right)\mathrm{dh} \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\mathrm{h}\:\mathrm{cot}\:\mathrm{h}\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{h}\right)\:\mathrm{dh}\: \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\mathrm{h}\left(\mathrm{cot}\:\mathrm{h}−\mathrm{tan}\:\mathrm{h}\right)\mathrm{dh}\: \\ $$$$\mathrm{by}\:\mathrm{parts},\:\mathrm{where}\:\mathrm{u}\:=\:\mathrm{h}\:,\:\mathrm{dv}\:=\:\left(\mathrm{cot}\:\mathrm{h}−\mathrm{tan}\:\mathrm{h}\right)\mathrm{dh} \\ $$$$\mathrm{I}=\mathrm{h}\left(\mathrm{ln}\left(\mathrm{sin}\:\mathrm{h}\right)+\mathrm{ln}\left(\mathrm{cos}\:\mathrm{h}\right)\right)\mid_{\mathrm{0}} ^{\pi/\mathrm{4}} −\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\mathrm{ln}\left(\mathrm{sin}\:\mathrm{h}\right)+\mathrm{ln}\left(\mathrm{cos}\:\mathrm{h}\right)\mathrm{dh} \\ $$$$\mathrm{I}=\:\mathrm{h}\:\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left(\mathrm{2h}\right)\right)\underset{\:\mathrm{0}} {\mid}^{\pi/\mathrm{4}} −\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left(\mathrm{2h}\right)\right)\mathrm{dh} \\ $$$$\mathrm{I}=−\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\left(−\mathrm{ln2}\:+\mathrm{ln}\left(\mathrm{sin}\:\left(\mathrm{2h}\right)\right)\right)\mathrm{dh} \\ $$$$\mathrm{I}=\:−\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\mathrm{ln}\left(\mathrm{sin}\:\left(\mathrm{2h}\right)\right)\mathrm{dh} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{ln}\left(\mathrm{sin}\:\mathrm{t}\right)\:\mathrm{dt}\:;\:\mathrm{via}\:\mathrm{t}\:=\:\mathrm{2h} \\ $$$$\mathrm{I}=\:−\frac{\mathrm{1}}{\mathrm{2}}.\:\left(−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\right)=\:\frac{\pi\:\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *