Question Number 37270 by abdo.msup.com last updated on 11/Jun/18
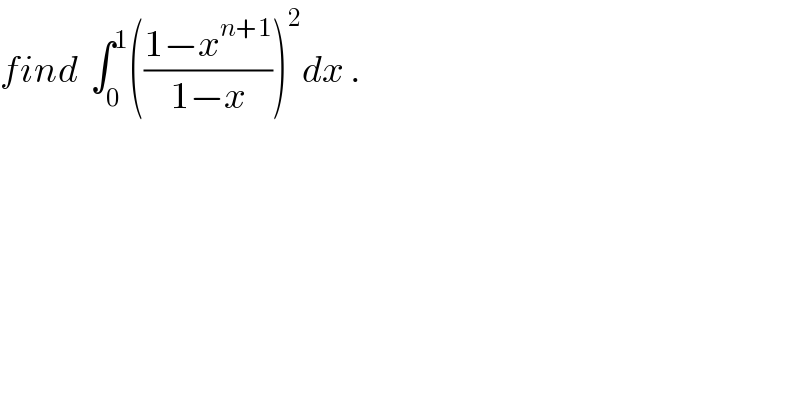
$${find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{\mathrm{1}−{x}}\right)^{\mathrm{2}} {dx}\:. \\ $$
Answered by abdo.msup.com last updated on 27/Jul/18
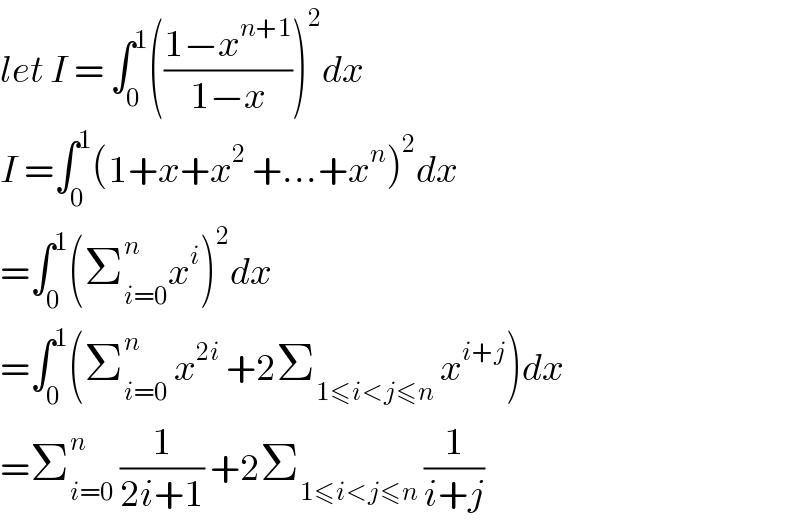
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{\mathrm{1}−{x}}\right)^{\mathrm{2}} {dx} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \:+…+{x}^{{n}} \right)^{\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{i}=\mathrm{0}} ^{{n}} {x}^{{i}} \right)^{\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{i}=\mathrm{0}} ^{{n}} \:{x}^{\mathrm{2}{i}} \:+\mathrm{2}\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:{x}^{{i}+{j}} \right){dx} \\ $$$$=\sum_{{i}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{i}+\mathrm{1}}\:+\mathrm{2}\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\frac{\mathrm{1}}{{i}+{j}} \\ $$
Commented by abdo.msup.com last updated on 27/Jul/18
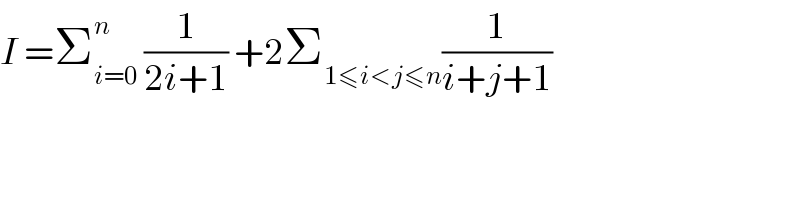
$${I}\:=\sum_{{i}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{i}+\mathrm{1}}\:+\mathrm{2}\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \frac{\mathrm{1}}{{i}+{j}+\mathrm{1}} \\ $$
