Question Number 37277 by abdo.msup.com last updated on 11/Jun/18
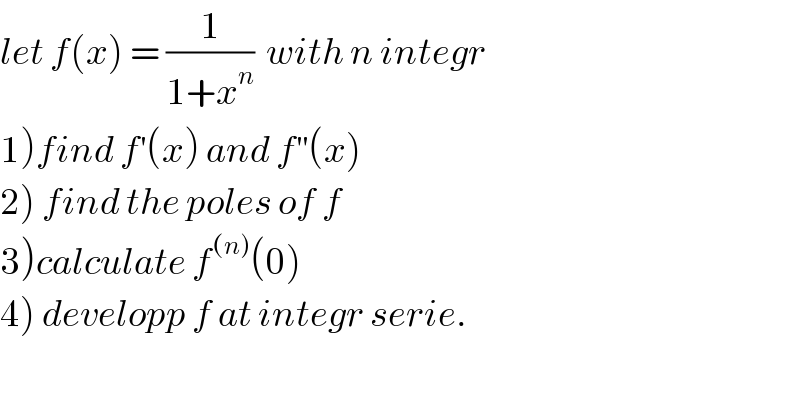
$${let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:\:{with}\:{n}\:{integr} \\ $$$$\left.\mathrm{1}\right){find}\:{f}^{'} \left({x}\right)\:{and}\:{f}^{''} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{poles}\:{of}\:{f} \\ $$$$\left.\mathrm{3}\right){calculate}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{4}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}. \\ $$
Commented by prof Abdo imad last updated on 16/Jun/18
![1)f^′ (x)=−((nx^(n−1) )/((1+x^n )^2 )) and f^(′′) (x)=−((n(n−1)x^(n−2) (1+x^n )^2 −2(1+x^n )nx^(n−1) nx^(n−1) )/((1+x^n )^4 )) =−((n(n−1)x^(n−2) (1+x^n )−2n^2 x^(2n−2) )/((1+x^n )^3 )) 2)z^n +1=0 ⇔ z^n =e^(iπ) so if z=re^(iθ) we get r=1 and nθ=(2k+1)π ⇒θ_k =(((2k+1)π)/n) so the poles of f are z_k =e^(i(((2k+1)π)/n)) and k ∈[[0,n−1]].](https://www.tinkutara.com/question/Q37682.png)
$$\left.\mathrm{1}\right){f}^{'} \left({x}\right)=−\frac{{nx}^{{n}−\mathrm{1}} }{\left(\mathrm{1}+{x}^{{n}} \right)^{\mathrm{2}} }\:{and} \\ $$$${f}^{''} \left({x}\right)=−\frac{{n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} \left(\mathrm{1}+{x}^{{n}} \right)^{\mathrm{2}} \:−\mathrm{2}\left(\mathrm{1}+{x}^{{n}} \right){nx}^{{n}−\mathrm{1}} {nx}^{{n}−\mathrm{1}} }{\left(\mathrm{1}+{x}^{{n}} \right)^{\mathrm{4}} } \\ $$$$=−\frac{{n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} \left(\mathrm{1}+{x}^{{n}} \right)−\mathrm{2}{n}^{\mathrm{2}} \:{x}^{\mathrm{2}{n}−\mathrm{2}} }{\left(\mathrm{1}+{x}^{{n}} \right)^{\mathrm{3}} } \\ $$$$\left.\mathrm{2}\right){z}^{{n}} \:+\mathrm{1}=\mathrm{0}\:\Leftrightarrow\:{z}^{{n}} ={e}^{{i}\pi} \:\:{so}\:{if}\:{z}={re}^{{i}\theta} \:{we}\:{get} \\ $$$${r}=\mathrm{1}\:{and}\:{n}\theta=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow\theta_{{k}} =\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}} \\ $$$${so}\:{the}\:{poles}\:{of}\:{f}\:{are}\:{z}_{{k}} ={e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} \\ $$$${and}\:{k}\:\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]. \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 16/Jun/18
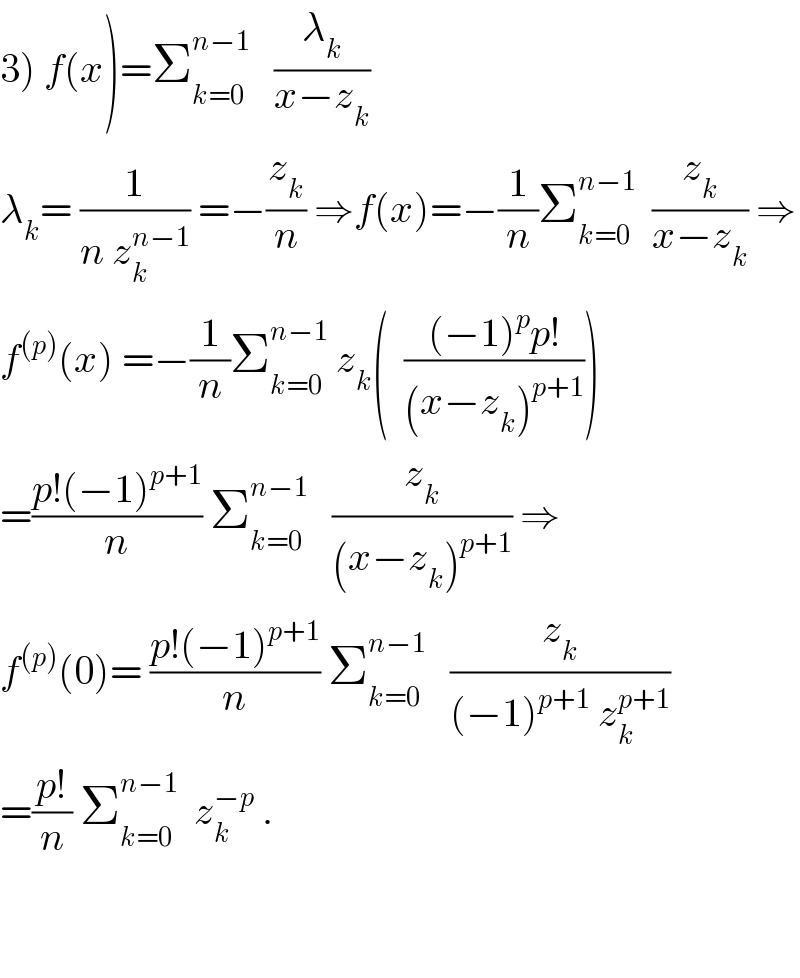
$$\left.\mathrm{3}\right)\:{f}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\lambda_{{k}} }{{x}−{z}_{{k}} } \\ $$$$\lambda_{{k}} =\:\frac{\mathrm{1}}{{n}\:{z}_{{k}} ^{{n}−\mathrm{1}} }\:=−\frac{{z}_{{k}} }{{n}}\:\Rightarrow{f}\left({x}\right)=−\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{{z}_{{k}} }{{x}−{z}_{{k}} }\:\Rightarrow \\ $$$${f}^{\left({p}\right)} \left({x}\right)\:=−\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{z}_{{k}} \left(\:\:\frac{\left(−\mathrm{1}\right)^{{p}} {p}!}{\left({x}−{z}_{{k}} \right)^{{p}+\mathrm{1}} }\right) \\ $$$$=\frac{{p}!\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} }{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{{z}_{{k}} }{\left({x}−{z}_{{k}} \right)^{{p}+\mathrm{1}} }\:\Rightarrow \\ $$$${f}^{\left({p}\right)} \left(\mathrm{0}\right)=\:\frac{{p}!\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} }{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{{z}_{{k}} }{\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} \:{z}_{{k}} ^{{p}+\mathrm{1}} } \\ $$$$=\frac{{p}!}{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{z}_{{k}} ^{−{p}} \:. \\ $$$$ \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 16/Jun/18
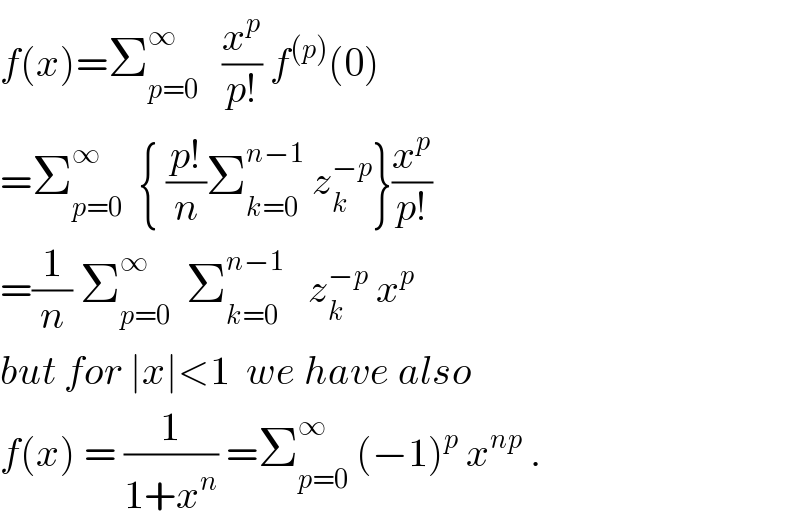
$${f}\left({x}\right)=\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{{p}} }{{p}!}\:{f}^{\left({p}\right)} \left(\mathrm{0}\right) \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\left\{\:\frac{{p}!}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{z}_{{k}} ^{−{p}} \right\}\frac{{x}^{{p}} }{{p}!} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:{z}_{{k}} ^{−{p}} \:{x}^{{p}} \\ $$$${but}\:{for}\:\mid{x}\mid<\mathrm{1}\:\:{we}\:{have}\:{also} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:=\sum_{{p}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{p}} \:{x}^{{np}} \:. \\ $$
