Menu Close

let-U-n-0-1-x-n-1-x-2n-1-dx-1-find-a-equivalent-of-U-n-n-2-study-the-comvergence-of-U-n-

Tinku Tara 0 Comments
Pin




Question Number 168355 by Mathspace last updated on 08/Apr/22
let U_n =∫_0 ^1 (x^n )(√(1−x^(2n+1) )))dx 1) find a equivalent of U_n (n∼∞) 2) study the comvergence of Σ U_n
$$\left.{let}\:{U}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{{n}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}{n}+\mathrm{1}} }\right){dx} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{equivalent}\:{of}\:{U}_{{n}} \left({n}\sim\infty\right) \\ $$$$\left.\mathrm{2}\right)\:{study}\:{the}\:{comvergence}\:{of}\:\Sigma\:{U}_{{n}} \\ $$
Answered by Mathspace last updated on 09/Apr/22
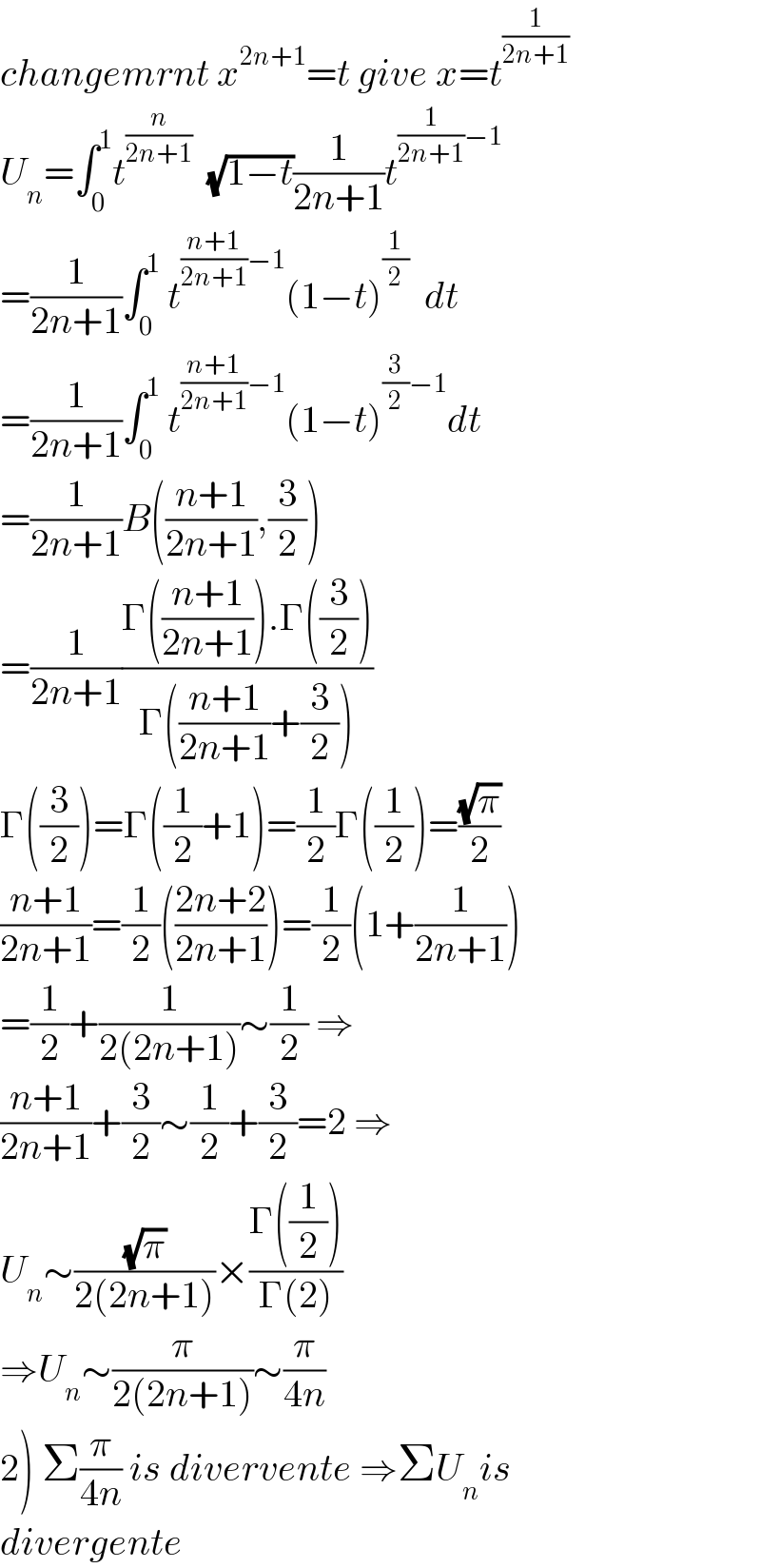
changemrnt x^(2n+1) =t give x=t^(1/(2n+1)) U_n =∫_0 ^1 t^(n/(2n+1)) (√(1−t))(1/(2n+1))t^((1/(2n+1))−1) =(1/(2n+1))∫_0 ^1 t^(((n+1)/(2n+1))−1) (1−t)^(1/2) dt =(1/(2n+1))∫_0 ^1 t^(((n+1)/(2n+1))−1) (1−t)^((3/2)−1) dt =(1/(2n+1))B(((n+1)/(2n+1)),(3/2)) =(1/(2n+1))((Γ(((n+1)/(2n+1))).Γ((3/2)))/(Γ(((n+1)/(2n+1))+(3/2)))) Γ((3/2))=Γ((1/2)+1)=(1/2)Γ((1/2))=((√π)/2) ((n+1)/(2n+1))=(1/2)(((2n+2)/(2n+1)))=(1/2)(1+(1/(2n+1))) =(1/2)+(1/(2(2n+1)))∼(1/2) ⇒ ((n+1)/(2n+1))+(3/2)∼(1/2)+(3/2)=2 ⇒ U_n ∼((√π)/(2(2n+1)))×((Γ((1/2)))/(Γ(2))) ⇒U_n ∼(π/(2(2n+1)))∼(π/(4n)) 2) Σ(π/(4n)) is divervente ⇒ΣU_n is divergente
$${changemrnt}\:{x}^{\mathrm{2}{n}+\mathrm{1}} ={t}\:{give}\:{x}={t}^{\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}} \\ $$$${U}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{{n}}{\mathrm{2}{n}+\mathrm{1}}} \:\:\sqrt{\mathrm{1}−{t}}\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{t}^{\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\frac{{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\frac{{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{B}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\frac{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\frac{{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}{n}+\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)}\sim\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{2}}\sim\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{2}\:\Rightarrow \\ $$$${U}_{{n}} \sim\frac{\sqrt{\pi}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)}×\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)} \\ $$$$\Rightarrow{U}_{{n}} \sim\frac{\pi}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)}\sim\frac{\pi}{\mathrm{4}{n}} \\ $$$$\left.\mathrm{2}\right)\:\Sigma\frac{\pi}{\mathrm{4}{n}}\:{is}\:{divervente}\:\Rightarrow\Sigma{U}_{{n}} {is} \\ $$$${divergente} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *