Question Number 37283 by abdo.msup.com last updated on 11/Jun/18
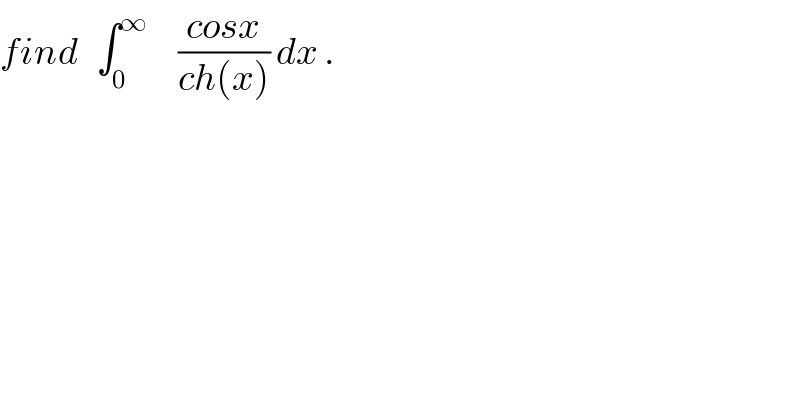
$${find}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{cosx}}{{ch}\left({x}\right)}\:{dx}\:. \\ $$
Commented by prof Abdo imad last updated on 16/Jun/18
![I = 2 ∫_0 ^∞ ((cosx)/(e^x +e^(−x) ))dx=2 ∫_0 ^∞ ((e^(−x) cosx)/(1+e^(−2x) ))dx =2 Re(∫_0 ^∞ (e^(−x+ix) /(1+e^(−2x) ))dx) ∫_0 ^∞ (e^(−x +ix) /(1+e^(−2x) ))dx =∫_0 ^∞ e^(−x+ix) (Σ_(n=0) ^∞ (−1)^n e^(−2nx) )dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^({−(2n+1)+i)x) dx but ∫_0 ^∞ e^({−(2n+1)+i}x) dx= (1/(−(2n+1) +i))[ e^({−(2n+1)+i}x) =]_0 ^(+∞) =((−1)/(−(2n+1)+i)) = (1/(2n+1−i)) =((2n+1 +i)/((2n+1)^(2 ) +1)) I =2Σ_(n=0) ^∞ (−1)^n ((2n+1)/((2n+1)^2 +1)) the value of this serie is known by using fourier serie ...be continued...](https://www.tinkutara.com/question/Q37678.png)
$${I}\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{cosx}}{{e}^{{x}} \:+{e}^{−{x}} }{dx}=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}} \:{cosx}}{\mathrm{1}+{e}^{−\mathrm{2}{x}} }{dx} \\ $$$$=\mathrm{2}\:{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−{x}+{ix}} }{\mathrm{1}+{e}^{−\mathrm{2}{x}} }{dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−{x}\:+{ix}} }{\mathrm{1}+{e}^{−\mathrm{2}{x}} }{dx}\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}+{ix}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{e}^{−\mathrm{2}{nx}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{\left\{−\left(\mathrm{2}{n}+\mathrm{1}\right)+{i}\right){x}} {dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{\left\{−\left(\mathrm{2}{n}+\mathrm{1}\right)+{i}\right\}{x}} {dx}=\:\frac{\mathrm{1}}{−\left(\mathrm{2}{n}+\mathrm{1}\right)\:+{i}}\left[\:{e}^{\left\{−\left(\mathrm{2}{n}+\mathrm{1}\right)+{i}\right\}{x}} =\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{−\mathrm{1}}{−\left(\mathrm{2}{n}+\mathrm{1}\right)+{i}}\:=\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}−{i}}\:=\frac{\mathrm{2}{n}+\mathrm{1}\:+{i}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}\:} \:+\mathrm{1}} \\ $$$${I}\:=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\:\frac{\mathrm{2}{n}+\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:{the}\:{value} \\ $$$${of}\:{this}\:{serie}\:{is}\:{known}\:{by}\:{using}\:{fourier}\:{serie} \\ $$$$…{be}\:{continued}… \\ $$$$ \\ $$
