Question Number 37310 by math khazana by abdo last updated on 11/Jun/18
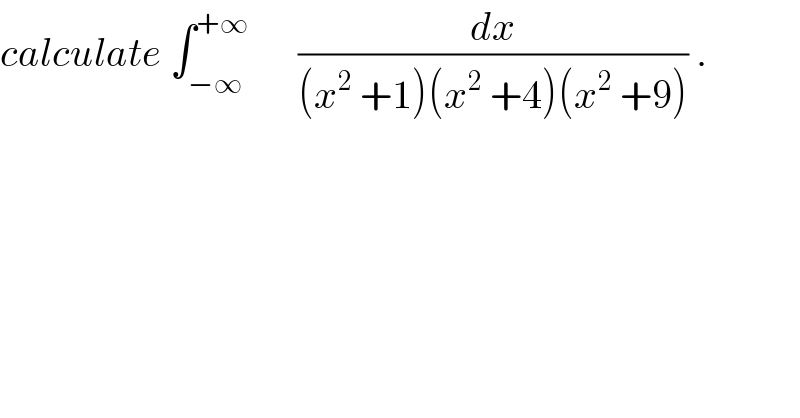
$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{4}\right)\left({x}^{\mathrm{2}} \:+\mathrm{9}\right)}\:. \\ $$
Commented by math khazana by abdo last updated on 12/Jun/18
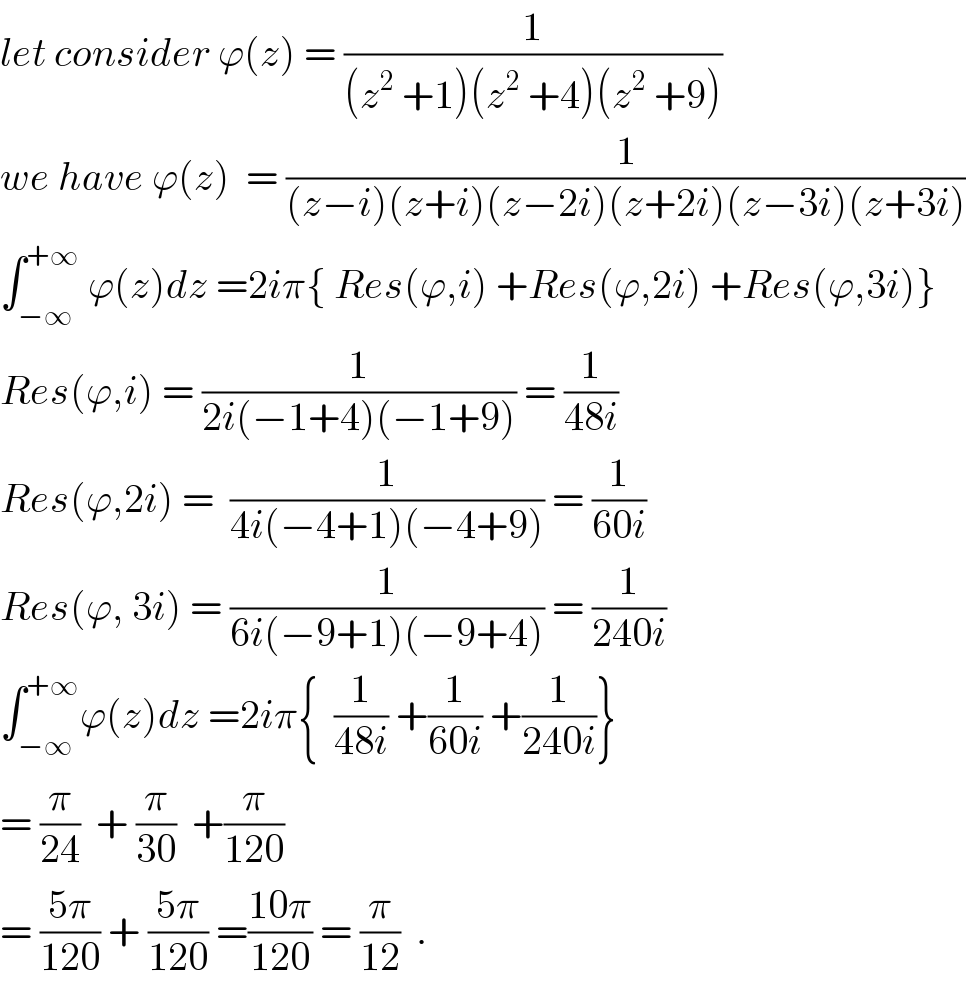
$${let}\:{consider}\:\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)\left({z}^{\mathrm{2}} \:+\mathrm{4}\right)\left({z}^{\mathrm{2}\:\:} +\mathrm{9}\right)} \\ $$$${we}\:{have}\:\varphi\left({z}\right)\:\:=\:\frac{\mathrm{1}}{\left({z}−{i}\right)\left({z}+{i}\right)\left({z}−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)\left({z}−\mathrm{3}{i}\right)\left({z}+\mathrm{3}{i}\right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{i}\right)\:+{Res}\left(\varphi,\mathrm{2}{i}\right)\:+{Res}\left(\varphi,\mathrm{3}{i}\right)\right\} \\ $$$${Res}\left(\varphi,{i}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}\left(−\mathrm{1}+\mathrm{4}\right)\left(−\mathrm{1}+\mathrm{9}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{48}{i}} \\ $$$${Res}\left(\varphi,\mathrm{2}{i}\right)\:=\:\:\frac{\mathrm{1}}{\mathrm{4}{i}\left(−\mathrm{4}+\mathrm{1}\right)\left(−\mathrm{4}+\mathrm{9}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{60}{i}} \\ $$$${Res}\left(\varphi,\:\mathrm{3}{i}\right)\:=\:\frac{\mathrm{1}}{\mathrm{6}{i}\left(−\mathrm{9}+\mathrm{1}\right)\left(−\mathrm{9}+\mathrm{4}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{240}{i}} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\:\frac{\mathrm{1}}{\mathrm{48}{i}}\:+\frac{\mathrm{1}}{\mathrm{60}{i}}\:+\frac{\mathrm{1}}{\mathrm{240}{i}}\right\} \\ $$$$=\:\frac{\pi}{\mathrm{24}}\:\:+\:\frac{\pi}{\mathrm{30}}\:\:+\frac{\pi}{\mathrm{120}}\:\:\:\:\:\: \\ $$$$=\:\frac{\mathrm{5}\pi}{\mathrm{120}}\:+\:\frac{\mathrm{5}\pi}{\mathrm{120}}\:=\frac{\mathrm{10}\pi}{\mathrm{120}}\:=\:\frac{\pi}{\mathrm{12}}\:\:. \\ $$
Answered by ajfour last updated on 11/Jun/18
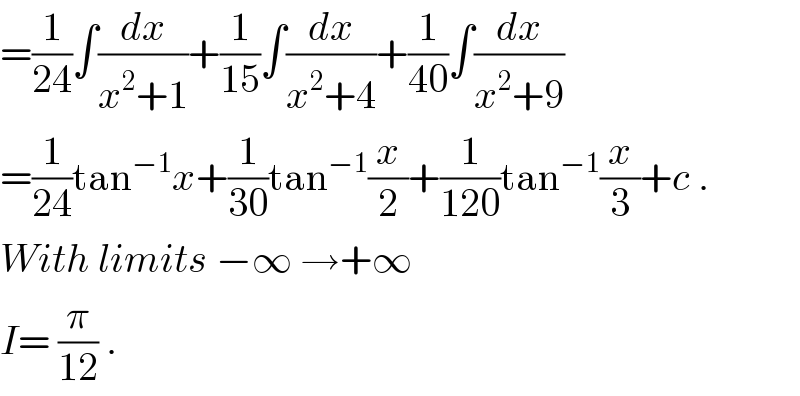
$$=\frac{\mathrm{1}}{\mathrm{24}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{15}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{40}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{9}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\mathrm{tan}^{−\mathrm{1}} {x}+\frac{\mathrm{1}}{\mathrm{30}}\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{120}}\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\mathrm{3}}+{c}\:. \\ $$$${With}\:{limits}\:−\infty\:\rightarrow+\infty \\ $$$${I}=\:\frac{\pi}{\mathrm{12}}\:. \\ $$
Commented by math khazana by abdo last updated on 12/Jun/18
$${correct}\:{answer}\:{thanks}\:{sir}\:{Ajfour} \\ $$
