Question Number 69188 by petrochengula last updated on 21/Sep/19

Commented by petrochengula last updated on 21/Sep/19

$$\mathrm{2}.{c}\:{help}\:{please} \\ $$
Commented by petrochengula last updated on 21/Sep/19

$$\mathrm{2}.{c}\:{help}\:{please} \\ $$
Answered by mr W last updated on 21/Sep/19
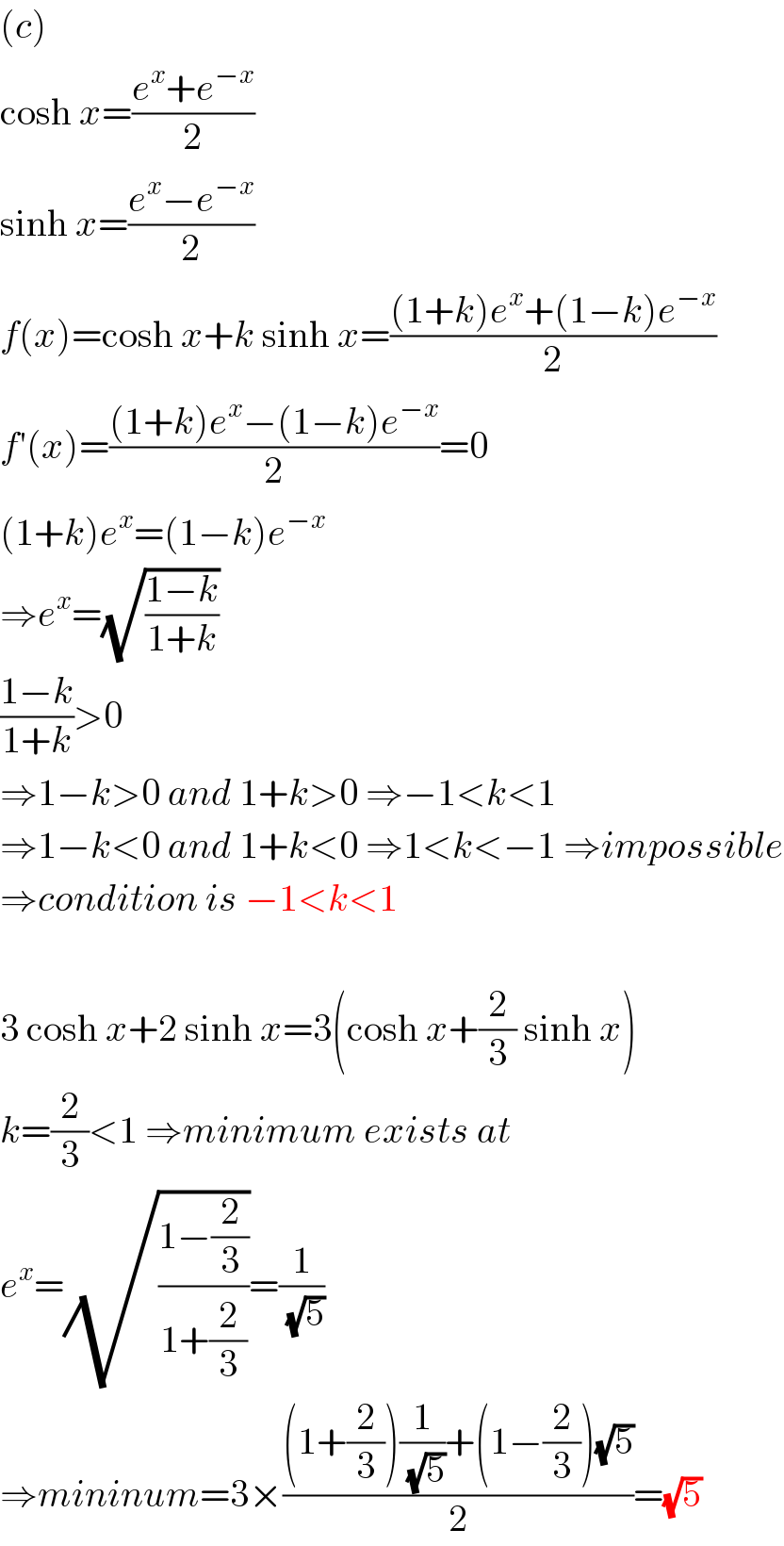
$$\left({c}\right) \\ $$$$\mathrm{cosh}\:{x}=\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}} \\ $$$$\mathrm{sinh}\:{x}=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}} \\ $$$${f}\left({x}\right)=\mathrm{cosh}\:{x}+{k}\:\mathrm{sinh}\:{x}=\frac{\left(\mathrm{1}+{k}\right){e}^{{x}} +\left(\mathrm{1}−{k}\right){e}^{−{x}} }{\mathrm{2}} \\ $$$${f}'\left({x}\right)=\frac{\left(\mathrm{1}+{k}\right){e}^{{x}} −\left(\mathrm{1}−{k}\right){e}^{−{x}} }{\mathrm{2}}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{k}\right){e}^{{x}} =\left(\mathrm{1}−{k}\right){e}^{−{x}} \\ $$$$\Rightarrow{e}^{{x}} =\sqrt{\frac{\mathrm{1}−{k}}{\mathrm{1}+{k}}} \\ $$$$\frac{\mathrm{1}−{k}}{\mathrm{1}+{k}}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−{k}>\mathrm{0}\:{and}\:\mathrm{1}+{k}>\mathrm{0}\:\Rightarrow−\mathrm{1}<{k}<\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}−{k}<\mathrm{0}\:{and}\:\mathrm{1}+{k}<\mathrm{0}\:\Rightarrow\mathrm{1}<{k}<−\mathrm{1}\:\Rightarrow{impossible} \\ $$$$\Rightarrow{condition}\:{is}\:−\mathrm{1}<{k}<\mathrm{1} \\ $$$$ \\ $$$$\mathrm{3}\:\mathrm{cosh}\:{x}+\mathrm{2}\:\mathrm{sinh}\:{x}=\mathrm{3}\left(\mathrm{cosh}\:{x}+\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{sinh}\:{x}\right) \\ $$$${k}=\frac{\mathrm{2}}{\mathrm{3}}<\mathrm{1}\:\Rightarrow{minimum}\:{exists}\:{at} \\ $$$${e}^{{x}} =\sqrt{\frac{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow{mininum}=\mathrm{3}×\frac{\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\right)\sqrt{\mathrm{5}}}{\mathrm{2}}=\sqrt{\mathrm{5}} \\ $$
Commented by petrochengula last updated on 21/Sep/19
thanks
Answered by Rio Michael last updated on 21/Sep/19

$$\mathrm{2}\left({a}\right)\:\:{let}\:{y}\:=\:{sinh}^{−\mathrm{1}} {x} \\ $$$$\Rightarrow\:{sinh}\:{y}\:=\:{x} \\ $$$$\frac{{e}^{{y}} −{e}^{−{y}} }{\mathrm{2}}\:=\:{x} \\ $$$${e}^{{y}} −{e}^{−{y}} =\:\mathrm{2}{x} \\ $$$${multiply}\:{all}\:{through}\:{by}\:\:{e}^{{y}} \\ $$$${e}^{\mathrm{2}{y}} −\:\mathrm{1}\:=\:\mathrm{2}{xe}^{{y}} \\ $$$${e}^{\mathrm{2}{y}} −\mathrm{2}{xe}^{{y}} −\mathrm{1}\:=\mathrm{0} \\ $$$${e}^{{y}} =\:\frac{\mathrm{2}{x}\pm\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\:\mathrm{4}}}{\mathrm{2}} \\ $$$${e}^{{y}} =\:\frac{\mathrm{2}{x}\pm\:\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}} \\ $$$${e}^{{y}} =\:{x}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${choose}\: \\ $$$$\:{e}^{{y}} \:=\:{x}\:+\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}\:=\:{ln}\:\left({x}\:+\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$${but}\:{y}\:=\:{sinh}^{−\mathrm{1}} {x} \\ $$$$\Rightarrow\:\:{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)\:=\:{ln}\:\left(\frac{\mathrm{3}}{\mathrm{4}}\:+\:\sqrt{\:\frac{\mathrm{9}}{\mathrm{16}}\:+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}\:+\:\sqrt{\frac{\mathrm{25}}{\mathrm{16}}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{ln}\:\left(\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{5}}{\mathrm{4}}\right)\:=\:{ln}\left(\mathrm{2}\right)\: \\ $$
