Question Number 37337 by math khazana by abdo last updated on 12/Jun/18
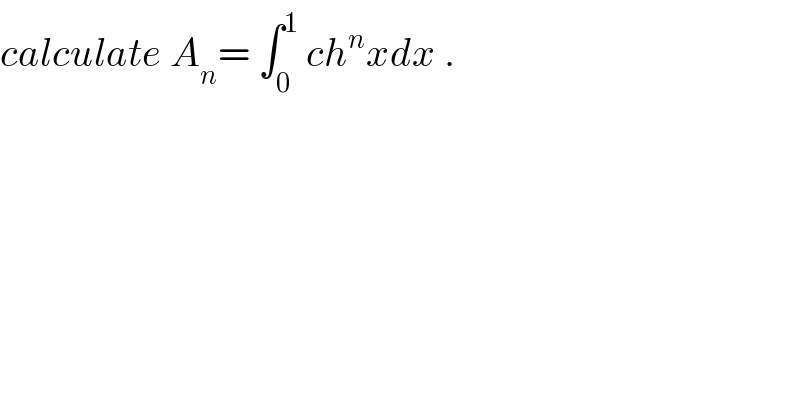
$${calculate}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ch}^{{n}} {xdx}\:. \\ $$
Commented by math khazana by abdo last updated on 13/Jun/18
![A_n = ∫_0 ^1 (((e^x +e^(−x) )/2))^n dx = (1/2^n ) ∫_0 ^1 (Σ_(k=0) ^n C_n ^k e^(kx) e^(−(n−k)x) )dx =(1/2^n ) Σ_(k=0) ^n C_n ^k ∫_0 ^1 e^((2k−n)x) dx =(1/2^n ) Σ_(k=0) ^n C_n ^k [(1/(2k−n)) e^((2k−n)x) ]_0 ^1 =(1/2^n ) Σ_(k=0) ^n (C_n ^k /(2k−n))( e^(2k−n) −1) .](https://www.tinkutara.com/question/Q37435.png)
$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{{e}^{{x}} \:+{e}^{−{x}} }{\mathrm{2}}\right)^{{n}} \:{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:{e}^{{kx}} \:{e}^{−\left({n}−{k}\right){x}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:{e}^{\left(\mathrm{2}{k}−{n}\right){x}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:\left[\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}\:{e}^{\left(\mathrm{2}{k}−{n}\right){x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{{C}_{{n}} ^{{k}} }{\mathrm{2}{k}−{n}}\left(\:{e}^{\mathrm{2}{k}−{n}} \:−\mathrm{1}\right)\:. \\ $$
