Menu Close

Question-102880

Tinku Tara 0 Comments
Pin




Question Number 102880 by Dwaipayan Shikari last updated on 11/Jul/20
Commented by Dwaipayan Shikari last updated on 11/Jul/20
Sorry sir . I did not include it . The weight recorder is mass less.The man stands on it.if Recorder records 72kg as the weight of the man the. Here the weight recorder is a trianguler platform. And it slides. Friction is along the slope
$${Sorry}\:{sir}\:.\:{I}\:{did}\:{not}\:{include}\:{it}\:.\:{The}\:{weight}\:{recorder}\:{is}\:{mass} \\ $$$${less}.{The}\:{man}\:{stands}\:{on}\:{it}.{if}\:{Recorder}\:{records}\:\mathrm{72}{kg}\:{as}\:{the} \\ $$$${weight}\:{of}\:{the}\:{man}\:{the}.\:{Here}\:{the}\:{weight}\:{recorder}\:{is}\:{a}\:{trianguler} \\ $$$${platform}.\:{And}\:{it}\:{slides}.\:{Friction}\:{is}\:{along}\:{the}\:{slope} \\ $$$$ \\ $$
Commented by mr W last updated on 11/Jul/20
do you understand based on the text how this recorder works and what the system does? does the man stand on the recorder which slideo along the wedge? can the wedge move on the ground? it talks about friction, which friction is meant? between the recorder and the wedge or elsewhere?
$${do}\:{you}\:{understand}\:{based}\:{on}\:{the}\:{text} \\ $$$${how}\:{this}\:{recorder}\:{works}\:{and}\:{what} \\ $$$${the}\:{system}\:{does}?\:{does}\:{the}\:{man} \\ $$$${stand}\:{on}\:{the}\:{recorder}\:{which}\:{slideo} \\ $$$${along}\:{the}\:{wedge}?\:{can}\:{the}\:{wedge}\:{move} \\ $$$${on}\:{the}\:{ground}?\:{it}\:{talks}\:{about} \\ $$$${friction},\:{which}\:{friction}\:{is}\:{meant}? \\ $$$${between}\:{the}\:{recorder}\:{and}\:{the}\:{wedge} \\ $$$${or}\:{elsewhere}? \\ $$
Commented by Dwaipayan Shikari last updated on 11/Jul/20
Commented by prakash jain last updated on 11/Jul/20
Can you use smaller lines. You may be using a tablet but most of us use phones.
$$\mathrm{Can}\:\mathrm{you}\:\mathrm{use}\:\mathrm{smaller}\:\mathrm{lines}.\:\mathrm{You}\:\mathrm{may} \\ $$$$\mathrm{be}\:\mathrm{using}\:\mathrm{a}\:\mathrm{tablet}\:\mathrm{but}\:\mathrm{most}\:\mathrm{of}\:\mathrm{us}\:\mathrm{use} \\ $$$$\mathrm{phones}. \\ $$
Commented by Dwaipayan Shikari last updated on 11/Jul/20
I will maintain it from the next time
$${I}\:{will}\:{maintain}\:{it}\:{from}\:{the}\:{next}\:{time} \\ $$
Answered by mr W last updated on 11/Jul/20
Commented by mr W last updated on 11/Jul/20
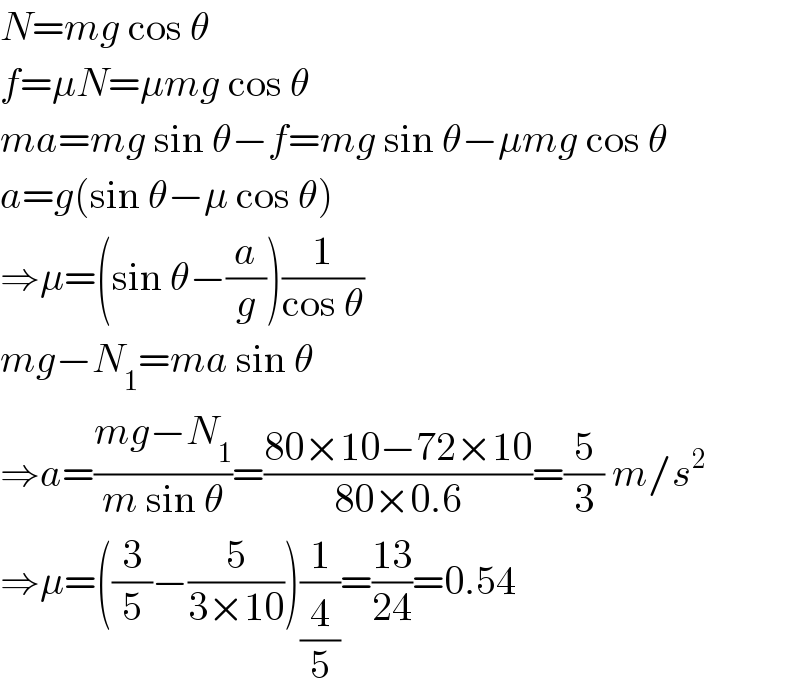
N=mg cos θ f=μN=μmg cos θ ma=mg sin θ−f=mg sin θ−μmg cos θ a=g(sin θ−μ cos θ) ⇒μ=(sin θ−(a/g))(1/(cos θ)) mg−N_1 =ma sin θ ⇒a=((mg−N_1 )/(m sin θ))=((80×10−72×10)/(80×0.6))=(5/3) m/s^2 ⇒μ=((3/5)−(5/(3×10)))(1/(4/5))=((13)/(24))=0.54
$${N}={mg}\:\mathrm{cos}\:\theta \\ $$$${f}=\mu{N}=\mu{mg}\:\mathrm{cos}\:\theta \\ $$$${ma}={mg}\:\mathrm{sin}\:\theta−{f}={mg}\:\mathrm{sin}\:\theta−\mu{mg}\:\mathrm{cos}\:\theta \\ $$$${a}={g}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\mu=\left(\mathrm{sin}\:\theta−\frac{{a}}{{g}}\right)\frac{\mathrm{1}}{\mathrm{cos}\:\theta} \\ $$$${mg}−{N}_{\mathrm{1}} ={ma}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{a}=\frac{{mg}−{N}_{\mathrm{1}} }{{m}\:\mathrm{sin}\:\theta}=\frac{\mathrm{80}×\mathrm{10}−\mathrm{72}×\mathrm{10}}{\mathrm{80}×\mathrm{0}.\mathrm{6}}=\frac{\mathrm{5}}{\mathrm{3}}\:{m}/{s}^{\mathrm{2}} \\ $$$$\Rightarrow\mu=\left(\frac{\mathrm{3}}{\mathrm{5}}−\frac{\mathrm{5}}{\mathrm{3}×\mathrm{10}}\right)\frac{\mathrm{1}}{\frac{\mathrm{4}}{\mathrm{5}}}=\frac{\mathrm{13}}{\mathrm{24}}=\mathrm{0}.\mathrm{54} \\ $$
Commented by mr W last updated on 11/Jul/20
Commented by Dwaipayan Shikari last updated on 11/Jul/20
Thanking you. Great!
$${Thanking}\:{you}.\:{Great}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *