Question Number 102883 by bobhans last updated on 11/Jul/20

$${If}\:{x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c}\:=\:\mathrm{0}\:{has}\:{the}\:{roots}\:{are}\: \\ $$$$\bar {\alpha}\:\beta\:{and}\:\gamma\:.\:{find}\:{the}\:{value}\:{of} \\ $$$$\alpha\beta^{\mathrm{2}} +\beta\gamma^{\mathrm{2}} +\gamma\alpha^{\mathrm{2}} \:{in}\:{terms}\:{a},{b}\:{and}\:{c} \\ $$
Answered by bemath last updated on 11/Jul/20
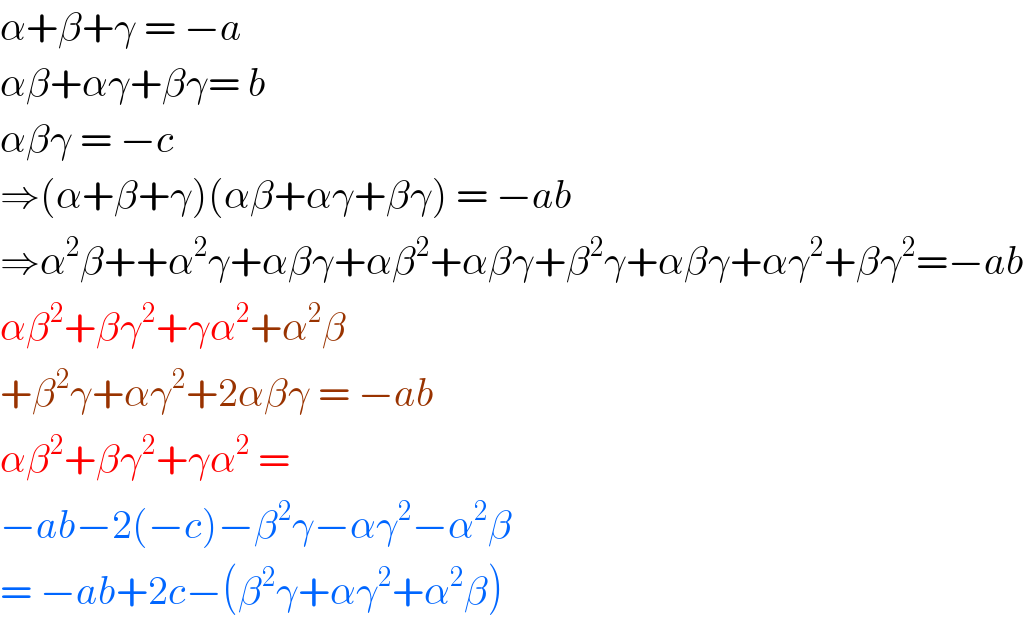
$$\alpha+\beta+\gamma\:=\:−{a} \\ $$$$\alpha\beta+\alpha\gamma+\beta\gamma=\:{b} \\ $$$$\alpha\beta\gamma\:=\:−{c}\: \\ $$$$\Rightarrow\left(\alpha+\beta+\gamma\right)\left(\alpha\beta+\alpha\gamma+\beta\gamma\right)\:=\:−{ab} \\ $$$$\Rightarrow\alpha^{\mathrm{2}} \beta++\alpha^{\mathrm{2}} \gamma+\alpha\beta\gamma+\alpha\beta^{\mathrm{2}} +\alpha\beta\gamma+\beta^{\mathrm{2}} \gamma+\alpha\beta\gamma+\alpha\gamma^{\mathrm{2}} +\beta\gamma^{\mathrm{2}} =−{ab} \\ $$$$\alpha\beta^{\mathrm{2}} +\beta\gamma^{\mathrm{2}} +\gamma\alpha^{\mathrm{2}} +\alpha^{\mathrm{2}} \beta \\ $$$$+\beta^{\mathrm{2}} \gamma+\alpha\gamma^{\mathrm{2}} +\mathrm{2}\alpha\beta\gamma\:=\:−{ab} \\ $$$$\alpha\beta^{\mathrm{2}} +\beta\gamma^{\mathrm{2}} +\gamma\alpha^{\mathrm{2}} \:= \\ $$$$−{ab}−\mathrm{2}\left(−{c}\right)−\beta^{\mathrm{2}} \gamma−\alpha\gamma^{\mathrm{2}} −\alpha^{\mathrm{2}} \beta \\ $$$$=\:−{ab}+\mathrm{2}{c}−\left(\beta^{\mathrm{2}} \gamma+\alpha\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} \beta\right) \\ $$
