Question Number 168427 by cortano1 last updated on 10/Apr/22
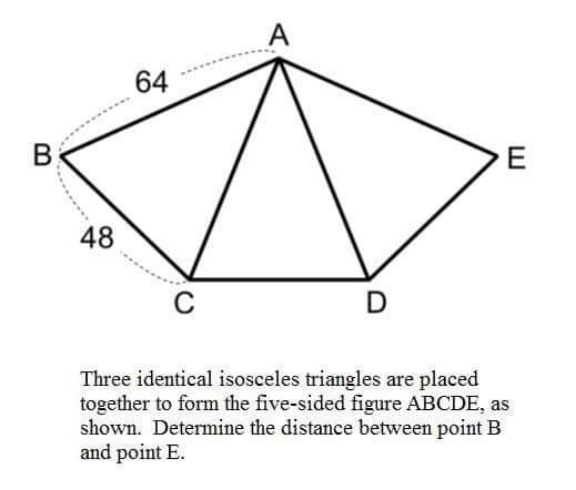
Commented by som(math1967) last updated on 10/Apr/22
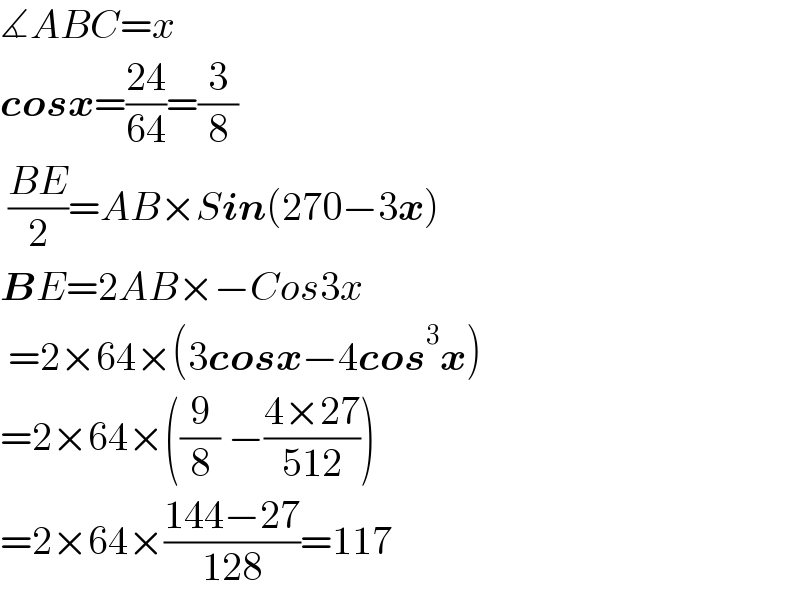
$$\measuredangle{ABC}={x} \\ $$$$\boldsymbol{{cosx}}=\frac{\mathrm{24}}{\mathrm{64}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\:\frac{{BE}}{\mathrm{2}}={AB}×{S}\boldsymbol{{in}}\left(\mathrm{270}−\mathrm{3}\boldsymbol{{x}}\right) \\ $$$$\boldsymbol{{B}}{E}=\mathrm{2}{AB}×−{Cos}\mathrm{3}{x} \\ $$$$\:=\mathrm{2}×\mathrm{64}×\left(\mathrm{3}\boldsymbol{{cosx}}−\mathrm{4}\boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{x}}\right) \\ $$$$=\mathrm{2}×\mathrm{64}×\left(\frac{\mathrm{9}}{\mathrm{8}}\:−\frac{\mathrm{4}×\mathrm{27}}{\mathrm{512}}\right) \\ $$$$=\mathrm{2}×\mathrm{64}×\frac{\mathrm{144}−\mathrm{27}}{\mathrm{128}}=\mathrm{117} \\ $$
Commented by som(math1967) last updated on 10/Apr/22
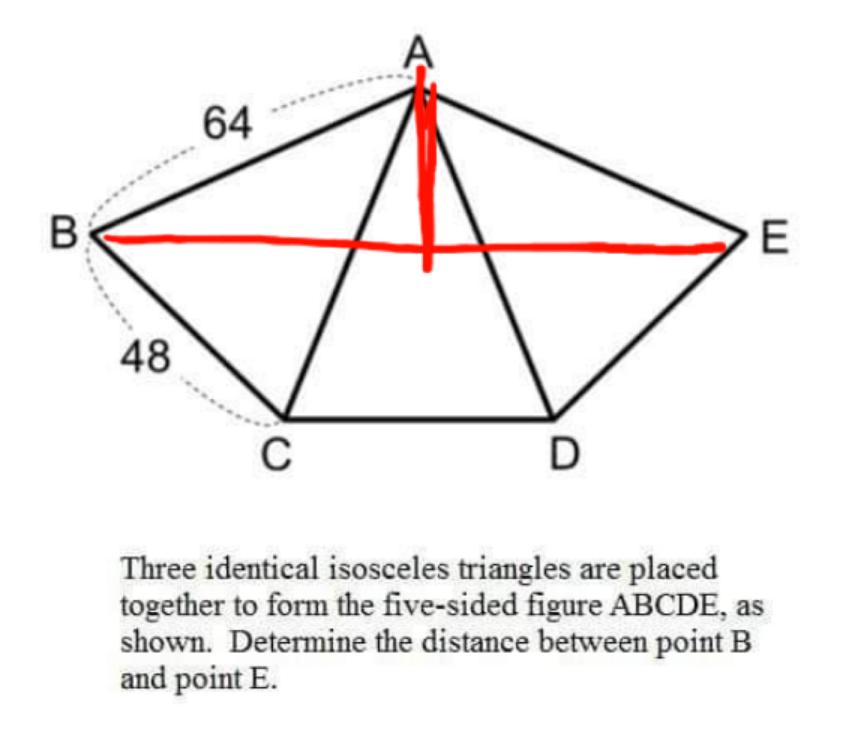
Answered by nikif99 last updated on 10/Apr/22
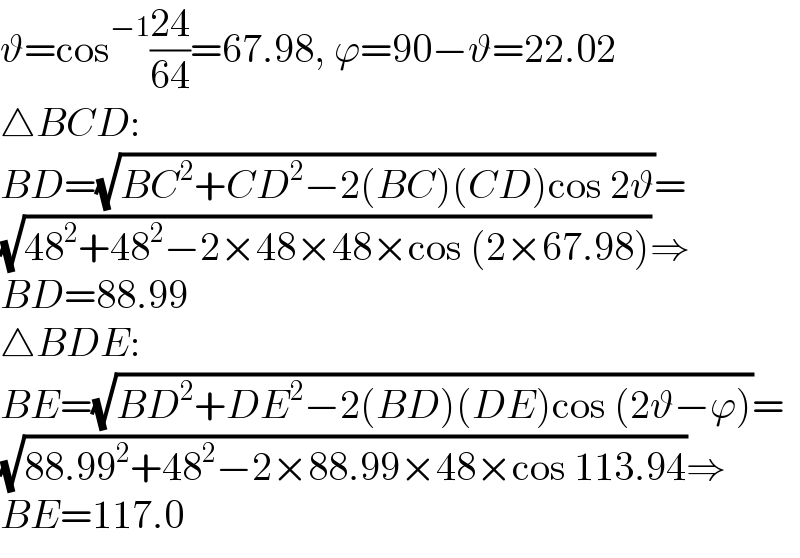
$$\vartheta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{24}}{\mathrm{64}}=\mathrm{67}.\mathrm{98},\:\varphi=\mathrm{90}−\vartheta=\mathrm{22}.\mathrm{02} \\ $$$$\bigtriangleup{BCD}: \\ $$$${BD}=\sqrt{{BC}^{\mathrm{2}} +{CD}^{\mathrm{2}} −\mathrm{2}\left({BC}\right)\left({CD}\right)\mathrm{cos}\:\mathrm{2}\vartheta}= \\ $$$$\sqrt{\mathrm{48}^{\mathrm{2}} +\mathrm{48}^{\mathrm{2}} −\mathrm{2}×\mathrm{48}×\mathrm{48}×\mathrm{cos}\:\left(\mathrm{2}×\mathrm{67}.\mathrm{98}\right)}\Rightarrow \\ $$$${BD}=\mathrm{88}.\mathrm{99} \\ $$$$\bigtriangleup{BDE}: \\ $$$${BE}=\sqrt{{BD}^{\mathrm{2}} +{DE}^{\mathrm{2}} −\mathrm{2}\left({BD}\right)\left({DE}\right)\mathrm{cos}\:\left(\mathrm{2}\vartheta−\varphi\right)}= \\ $$$$\sqrt{\mathrm{88}.\mathrm{99}^{\mathrm{2}} +\mathrm{48}^{\mathrm{2}} −\mathrm{2}×\mathrm{88}.\mathrm{99}×\mathrm{48}×\mathrm{cos}\:\mathrm{113}.\mathrm{94}}\Rightarrow \\ $$$${BE}=\mathrm{117}.\mathrm{0} \\ $$
Commented by nikif99 last updated on 10/Apr/22
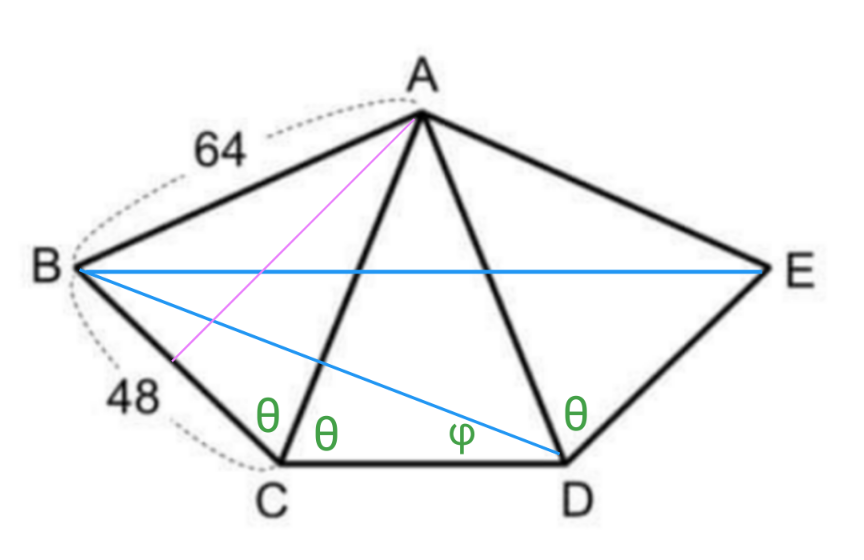
Answered by mr W last updated on 10/Apr/22
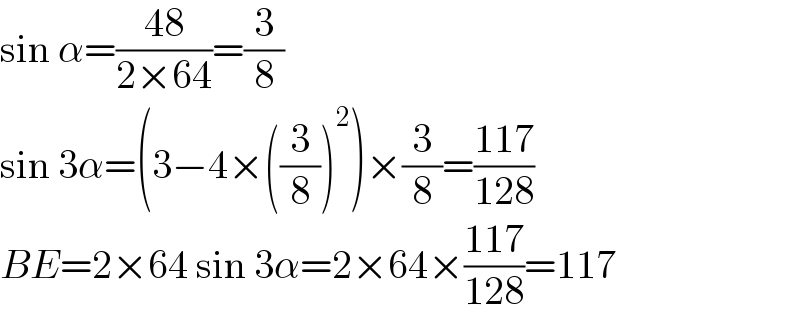
$$\mathrm{sin}\:\alpha=\frac{\mathrm{48}}{\mathrm{2}×\mathrm{64}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\mathrm{sin}\:\mathrm{3}\alpha=\left(\mathrm{3}−\mathrm{4}×\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{2}} \right)×\frac{\mathrm{3}}{\mathrm{8}}=\frac{\mathrm{117}}{\mathrm{128}} \\ $$$${BE}=\mathrm{2}×\mathrm{64}\:\mathrm{sin}\:\mathrm{3}\alpha=\mathrm{2}×\mathrm{64}×\frac{\mathrm{117}}{\mathrm{128}}=\mathrm{117} \\ $$
