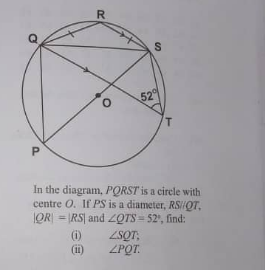
Question Number 102918 by otchereabdullai@gmail.com last updated on 11/Jul/20
Commented by bramlex last updated on 12/Jul/20
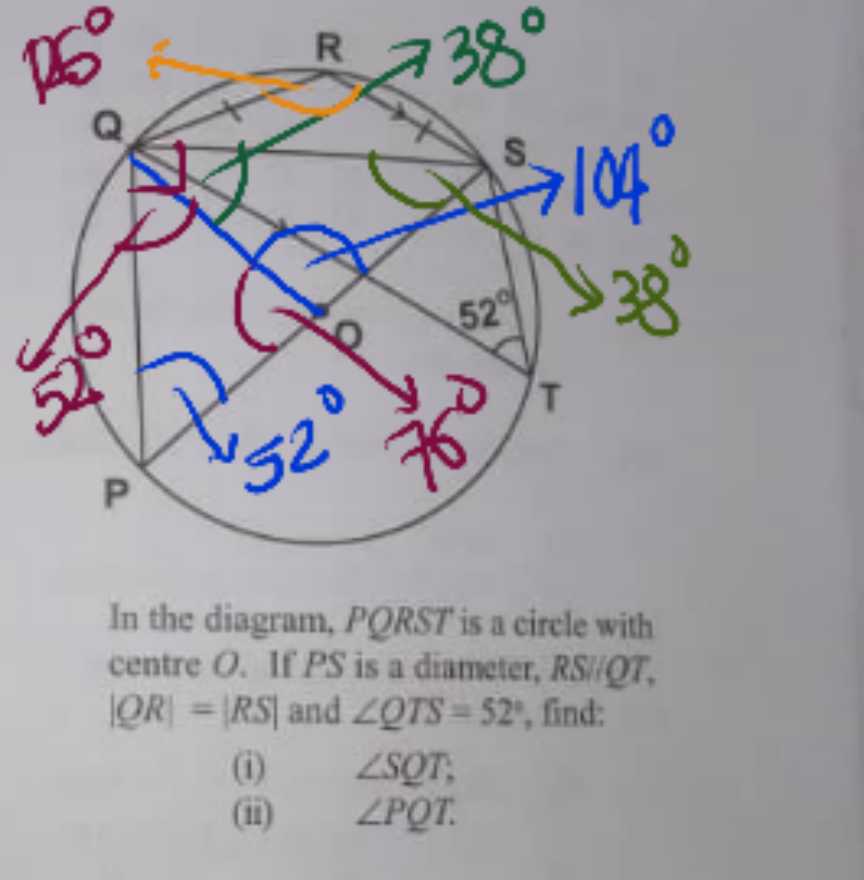
Commented by otchereabdullai@gmail.com last updated on 14/Jul/20
$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{ur}\:\mathrm{time}\:\mathrm{sir}\:! \\ $$
Answered by som(math1967) last updated on 11/Jul/20
![∠QTS=∠SPQ=52° ★ ∴∠QPS=180−52=128°■ ∠RQS=∠RSQ=((180−128)/2)=26°■■ ∠RSQ=∠SQT=26° ans ∠SQP=90° [semicirular angle] ∴∠PQT=∠SQP−∠SQT =90−26=64°ans ★subtain on same segment ■PQRS cyclic ■■QR=RS](https://www.tinkutara.com/question/Q102950.png)
$$\angle\mathrm{QTS}=\angle\mathrm{SPQ}=\mathrm{52}°\:\bigstar \\ $$$$\therefore\angle\mathrm{QPS}=\mathrm{180}−\mathrm{52}=\mathrm{128}°\blacksquare \\ $$$$\angle\mathrm{RQS}=\angle\mathrm{RSQ}=\frac{\mathrm{180}−\mathrm{128}}{\mathrm{2}}=\mathrm{26}°\blacksquare\blacksquare \\ $$$$\angle\mathrm{RSQ}=\angle\mathrm{SQT}=\mathrm{26}°\:\mathrm{ans} \\ $$$$\angle\mathrm{SQP}=\mathrm{90}°\:\left[\mathrm{semicirular}\right. \\ $$$$\left.\mathrm{angle}\right] \\ $$$$\therefore\angle\mathrm{PQT}=\angle\mathrm{SQP}−\angle\mathrm{SQT} \\ $$$$=\mathrm{90}−\mathrm{26}=\mathrm{64}°\mathrm{ans} \\ $$$$\bigstar\mathrm{subtain}\:\mathrm{on}\:\mathrm{same}\:\mathrm{segment} \\ $$$$\blacksquare\mathrm{PQRS}\:\mathrm{cyclic} \\ $$$$\blacksquare\blacksquare\mathrm{QR}=\mathrm{RS} \\ $$$$ \\ $$
Commented by otchereabdullai@gmail.com last updated on 11/Jul/20
$$\mathrm{God}\:\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}!\:\mathrm{Am}\:\mathrm{much}\:\mathrm{greatful} \\ $$$$\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$
