Question Number 168515 by cortano1 last updated on 12/Apr/22
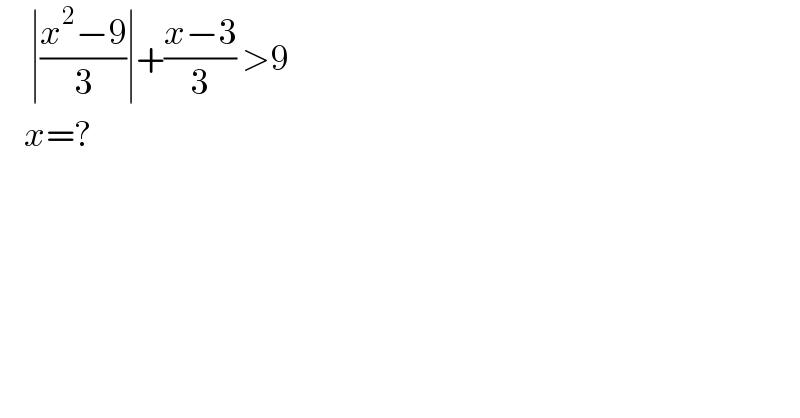
$$\:\:\:\:\:\mid\frac{{x}^{\mathrm{2}} −\mathrm{9}}{\mathrm{3}}\mid+\frac{{x}−\mathrm{3}}{\mathrm{3}}\:>\mathrm{9}\: \\ $$$$\:\:\:\:{x}=? \\ $$
Commented by benhamimed last updated on 12/Apr/22
![{ ((x^2 +x−39>0 si x∈]−∞;−3]∪[3;+∞[)),((−x^2 +x−21>0 si x∈[−3;3])) :} S=]−∞;((−1−(√(157)))/2)[∪]((−1+(√(157)))/2);+∞[](https://www.tinkutara.com/question/Q168517.png)
$$\begin{cases}{\left.{x}^{\mathrm{2}} \left.+{x}−\mathrm{39}>\mathrm{0}\:\:\:\:{si}\:{x}\in\right]−\infty;−\mathrm{3}\right]\cup\left[\mathrm{3};+\infty\left[\right.\right.}\\{−{x}^{\mathrm{2}} +{x}−\mathrm{21}>\mathrm{0}\:\:{si}\:\:{x}\in\left[−\mathrm{3};\mathrm{3}\right]}\end{cases} \\ $$$$\left.{S}=\right]−\infty;\frac{−\mathrm{1}−\sqrt{\mathrm{157}}}{\mathrm{2}}\left[\cup\right]\frac{−\mathrm{1}+\sqrt{\mathrm{157}}}{\mathrm{2}};+\infty\left[\right. \\ $$$$ \\ $$
Answered by Mathspace last updated on 12/Apr/22
![⇒((∣x^2 −9∣)/3)+((x−3)/3)>9 ⇒ ∣x^2 −9∣+x−3>27? ⇒ ∣x^2 −9∣+x−3−27>0 ⇒ ∣x^2 −9∣+x−30>0 f(x)=∣x^2 −9∣+x−30 x −∞ −3 3 +∞ ∣x^2 −9 x^2 −9 9−x^2 x^2 −9 x≤−3 ⇒f(x)=x^2 −9+x−30 =x^2 +x−39 x∈[−3,3] ⇒f(x)=9−x^2 +x−30 =−x^2 +x−21 x∈[3,+∞[ ⇒f(x)=x^2 −9+x−30 =x^2 +x−39 case 1 x≤−3 f>0 ⇒x^2 +x−39>0 Δ=1−4.(−39)=1+4.39 =1+156=157 x_1 =((−1+(√(157)))/2) x_2 =((−1−(√(157)))/2) ....](https://www.tinkutara.com/question/Q168533.png)
$$\Rightarrow\frac{\mid{x}^{\mathrm{2}} −\mathrm{9}\mid}{\mathrm{3}}+\frac{{x}−\mathrm{3}}{\mathrm{3}}>\mathrm{9}\:\Rightarrow \\ $$$$\mid{x}^{\mathrm{2}} −\mathrm{9}\mid+{x}−\mathrm{3}>\mathrm{27}?\:\Rightarrow \\ $$$$\mid{x}^{\mathrm{2}} −\mathrm{9}\mid+{x}−\mathrm{3}−\mathrm{27}>\mathrm{0}\:\Rightarrow \\ $$$$\mid{x}^{\mathrm{2}} −\mathrm{9}\mid+{x}−\mathrm{30}>\mathrm{0} \\ $$$${f}\left({x}\right)=\mid{x}^{\mathrm{2}} −\mathrm{9}\mid+{x}−\mathrm{30} \\ $$$${x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:−\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\mid{x}^{\mathrm{2}} −\mathrm{9}\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{9}\:\:\:\:\:\mathrm{9}−{x}^{\mathrm{2}} \:\:\:{x}^{\mathrm{2}} −\mathrm{9} \\ $$$${x}\leqslant−\mathrm{3}\:\Rightarrow{f}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{9}+{x}−\mathrm{30} \\ $$$$={x}^{\mathrm{2}} +{x}−\mathrm{39} \\ $$$${x}\in\left[−\mathrm{3},\mathrm{3}\right]\:\:\Rightarrow{f}\left({x}\right)=\mathrm{9}−{x}^{\mathrm{2}} +{x}−\mathrm{30} \\ $$$$=−{x}^{\mathrm{2}} +{x}−\mathrm{21} \\ $$$${x}\in\left[\mathrm{3},+\infty\left[\:\Rightarrow{f}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{9}+{x}−\mathrm{30}\right.\right. \\ $$$$={x}^{\mathrm{2}} +{x}−\mathrm{39} \\ $$$${case}\:\mathrm{1}\:\:\:{x}\leqslant−\mathrm{3} \\ $$$${f}>\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} +{x}−\mathrm{39}>\mathrm{0} \\ $$$$\Delta=\mathrm{1}−\mathrm{4}.\left(−\mathrm{39}\right)=\mathrm{1}+\mathrm{4}.\mathrm{39} \\ $$$$=\mathrm{1}+\mathrm{156}=\mathrm{157} \\ $$$${x}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{157}}}{\mathrm{2}} \\ $$$${x}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{157}}}{\mathrm{2}} \\ $$$$…. \\ $$$$ \\ $$
