Question Number 103008 by bobhans last updated on 12/Jul/20
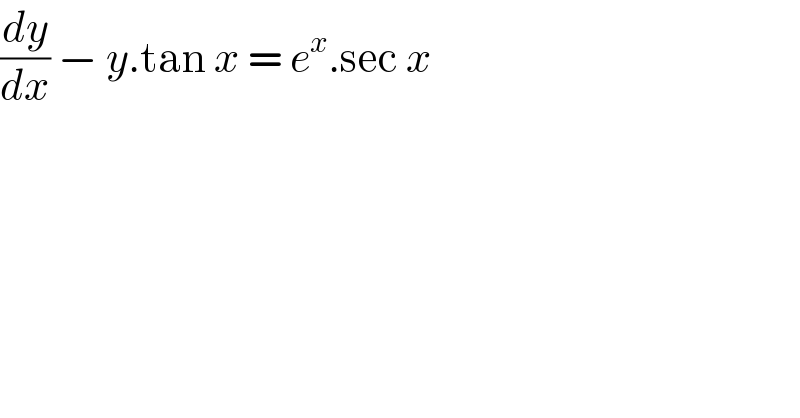
$$\frac{{dy}}{{dx}}\:−\:{y}.\mathrm{tan}\:{x}\:=\:{e}^{{x}} .\mathrm{sec}\:{x} \\ $$
Answered by bemath last updated on 12/Jul/20
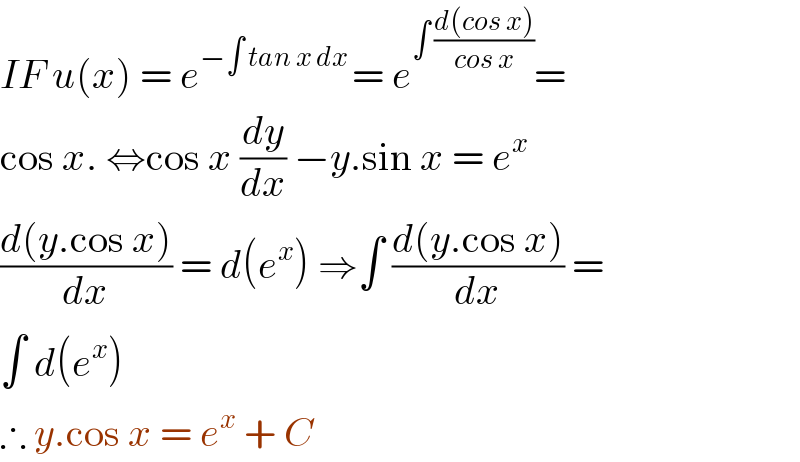
$${IF}\:{u}\left({x}\right)\:=\:{e}^{−\int\:{tan}\:{x}\:{dx}\:} =\:{e}^{\int\:\frac{{d}\left({cos}\:{x}\right)}{{cos}\:{x}}} = \\ $$$$\mathrm{cos}\:{x}.\:\Leftrightarrow\mathrm{cos}\:{x}\:\frac{{dy}}{{dx}}\:−{y}.\mathrm{sin}\:{x}\:=\:{e}^{{x}} \\ $$$$\frac{{d}\left({y}.\mathrm{cos}\:{x}\right)}{{dx}}\:=\:{d}\left({e}^{{x}} \right)\:\Rightarrow\int\:\frac{{d}\left({y}.\mathrm{cos}\:{x}\right)}{{dx}}\:= \\ $$$$\int\:{d}\left({e}^{{x}} \right)\: \\ $$$$\therefore\:{y}.\mathrm{cos}\:{x}\:=\:{e}^{{x}} \:+\:{C}\: \\ $$
Answered by mathmax by abdo last updated on 12/Jul/20
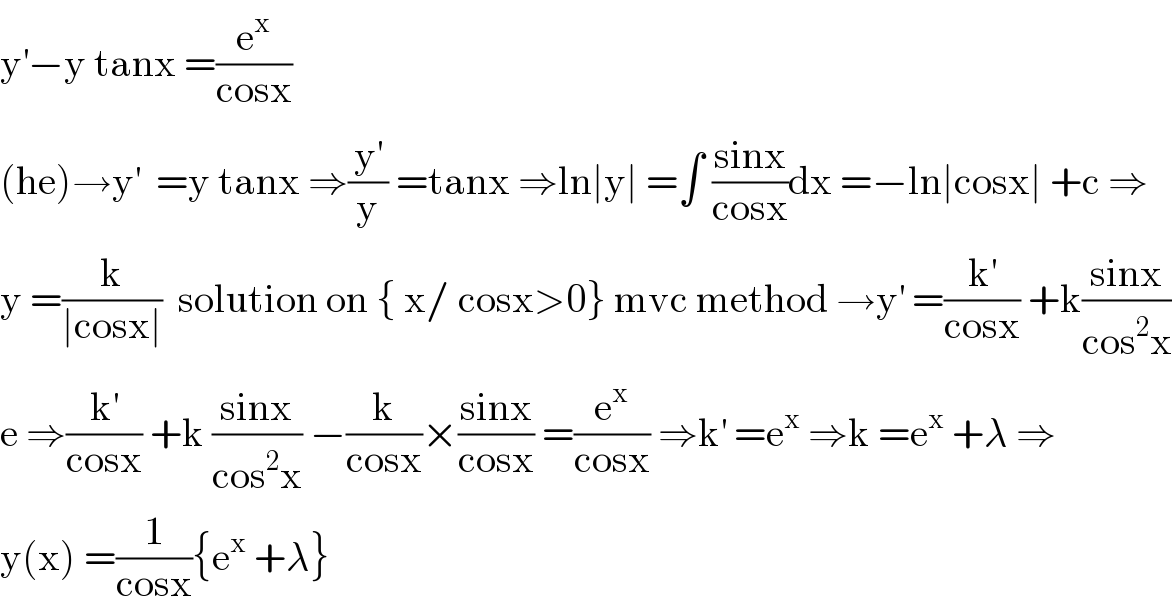
$$\mathrm{y}^{'} −\mathrm{y}\:\mathrm{tanx}\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{cosx}} \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{'} \:\:=\mathrm{y}\:\mathrm{tanx}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=\mathrm{tanx}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=\int\:\frac{\mathrm{sinx}}{\mathrm{cosx}}\mathrm{dx}\:=−\mathrm{ln}\mid\mathrm{cosx}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\:=\frac{\mathrm{k}}{\mid\mathrm{cosx}\mid}\:\:\mathrm{solution}\:\mathrm{on}\:\left\{\:\mathrm{x}/\:\mathrm{cosx}>\mathrm{0}\right\}\:\mathrm{mvc}\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\frac{\mathrm{k}^{'} }{\mathrm{cosx}}\:+\mathrm{k}\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}} \\ $$$$\mathrm{e}\:\Rightarrow\frac{\mathrm{k}^{'} }{\mathrm{cosx}}\:+\mathrm{k}\:\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:−\frac{\mathrm{k}}{\mathrm{cosx}}×\frac{\mathrm{sinx}}{\mathrm{cosx}}\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{cosx}}\:\Rightarrow\mathrm{k}^{'} \:=\mathrm{e}^{\mathrm{x}} \:\Rightarrow\mathrm{k}\:=\mathrm{e}^{\mathrm{x}} \:+\lambda\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{cosx}}\left\{\mathrm{e}^{\mathrm{x}} \:+\lambda\right\} \\ $$
Commented by bemath last updated on 12/Jul/20

$${what}\:\left({he}\right)\:{sir}? \\ $$
Commented by abdomsup last updated on 12/Jul/20
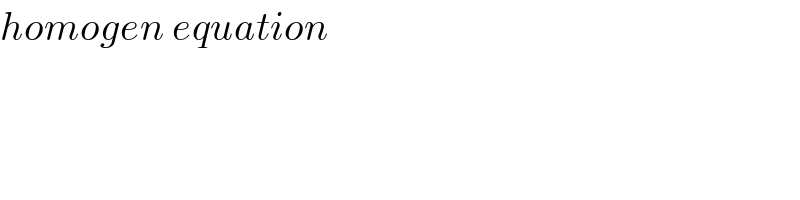
$${homogen}\:{equation} \\ $$
