Question Number 37485 by ajfour last updated on 13/Jun/18
Commented by ajfour last updated on 13/Jun/18
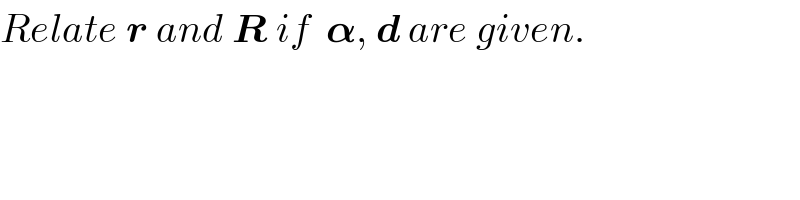
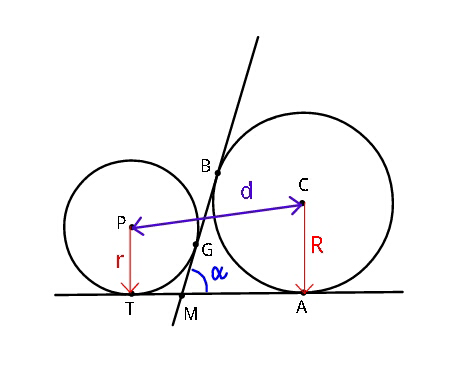
$${Relate}\:\boldsymbol{{r}}\:{and}\:\boldsymbol{{R}}\:{if}\:\:\boldsymbol{\alpha},\:\boldsymbol{{d}}\:{are}\:{given}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jun/18
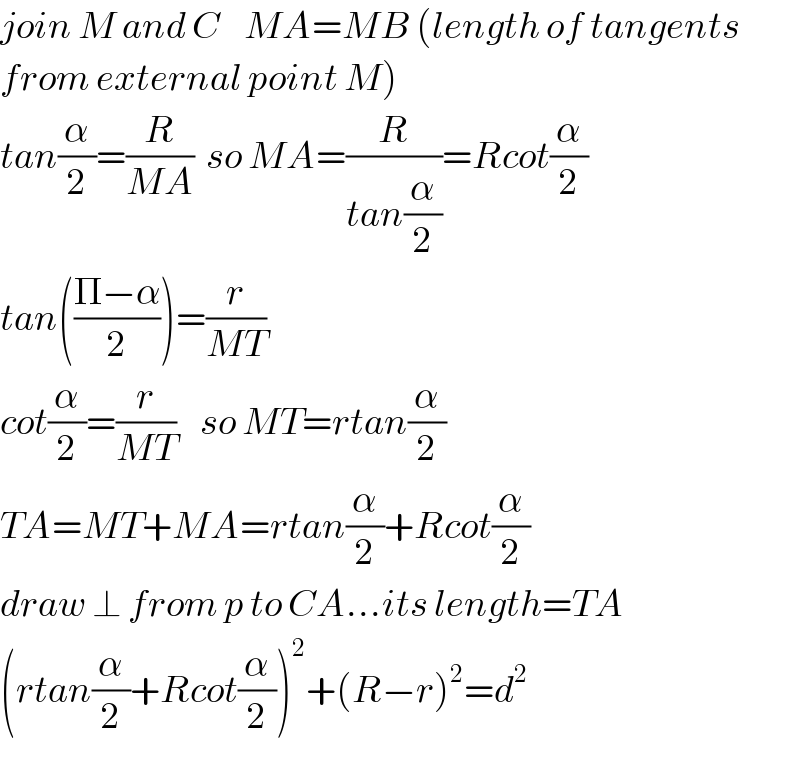
$${join}\:{M}\:{and}\:{C}\:\:\:\:{MA}={MB}\:\left({length}\:{of}\:{tangents}\right. \\ $$$$\left.{from}\:{external}\:{point}\:{M}\right) \\ $$$${tan}\frac{\alpha}{\mathrm{2}}=\frac{{R}}{{MA}}\:\:{so}\:{MA}=\frac{{R}}{{tan}\frac{\alpha}{\mathrm{2}}}={Rcot}\frac{\alpha}{\mathrm{2}} \\ $$$${tan}\left(\frac{\Pi−\alpha}{\mathrm{2}}\right)=\frac{{r}}{{MT}}\:\:\: \\ $$$${cot}\frac{\alpha}{\mathrm{2}}=\frac{{r}}{{MT}}\:\:\:\:{so}\:{MT}={rtan}\frac{\alpha}{\mathrm{2}} \\ $$$${TA}={MT}+{MA}={rtan}\frac{\alpha}{\mathrm{2}}+{Rcot}\frac{\alpha}{\mathrm{2}} \\ $$$${draw}\:\bot\:{from}\:{p}\:{to}\:{CA}…{its}\:{length}={TA} \\ $$$$\left({rtan}\frac{\alpha}{\mathrm{2}}+{Rcot}\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} +\left({R}−{r}\right)^{\mathrm{2}} ={d}^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 14/Jun/18

$${thanks}\:{sir}.\: \\ $$
Answered by behi83417@gmail.com last updated on 13/Jun/18
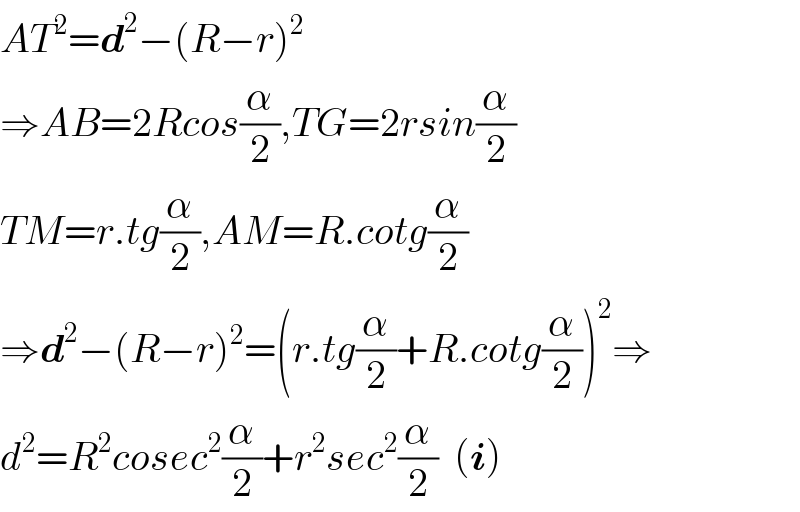
$${AT}^{\mathrm{2}} =\boldsymbol{{d}}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{AB}=\mathrm{2}{Rcos}\frac{\alpha}{\mathrm{2}},{TG}=\mathrm{2}{rsin}\frac{\alpha}{\mathrm{2}} \\ $$$${TM}={r}.{tg}\frac{\alpha}{\mathrm{2}},{AM}={R}.{cotg}\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{{d}}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} =\left({r}.{tg}\frac{\alpha}{\mathrm{2}}+{R}.{cotg}\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \Rightarrow \\ $$$${d}^{\mathrm{2}} ={R}^{\mathrm{2}} {cosec}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}+{r}^{\mathrm{2}} {sec}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}\:\:\left(\boldsymbol{{i}}\right) \\ $$
Commented by ajfour last updated on 14/Jun/18

$${thank}\:{you}\:{sir}. \\ $$
