Question Number 103047 by bemath last updated on 12/Jul/20

$${find}\:{the}\:{product}\:{of}\:{roots}\: \\ $$$$\sqrt[{\mathrm{3}\:}]{\mathrm{2021}}\:{x}^{\mathrm{log}_{\mathrm{2021}} \:\left({x}\right)} \:=\:{x}^{\mathrm{3}} \\ $$
Commented by mr W last updated on 12/Jul/20

$$\Pi{x}=\mathrm{2021}^{\mathrm{3}} \:? \\ $$
Answered by floor(10²Eta[1]) last updated on 12/Jul/20

$$\mathrm{log}_{\mathrm{2021}} \left(\mathrm{x}\right)=\mathrm{y}\Rightarrow\mathrm{x}=\mathrm{2021}^{\mathrm{y}} \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\mathrm{2021}}.\left(\mathrm{2021}^{\mathrm{y}} \right)^{\mathrm{y}} =\left(\mathrm{2021}^{\mathrm{y}} \right)^{\mathrm{3}} \\ $$$$\mathrm{2021}^{\mathrm{1}/\mathrm{3}} .\mathrm{2021}^{\mathrm{y}^{\mathrm{2}} } =\mathrm{2021}^{\mathrm{3y}} \\ $$$$\Rightarrow\mathrm{y}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{3y}\Rightarrow\mathrm{y}^{\mathrm{2}} −\mathrm{3y}+\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{product}=\mathrm{x}_{\mathrm{1}} .\mathrm{x}_{\mathrm{2}} =\mathrm{2021}^{\mathrm{y}_{\mathrm{1}} } .\mathrm{2021}^{\mathrm{y}_{\mathrm{2}} } \\ $$$$=\mathrm{2021}^{\mathrm{y}_{\mathrm{1}} +\mathrm{y}_{\mathrm{2}} } =\mathrm{2021}^{\mathrm{3}} \\ $$
Answered by bemath last updated on 14/Jul/20
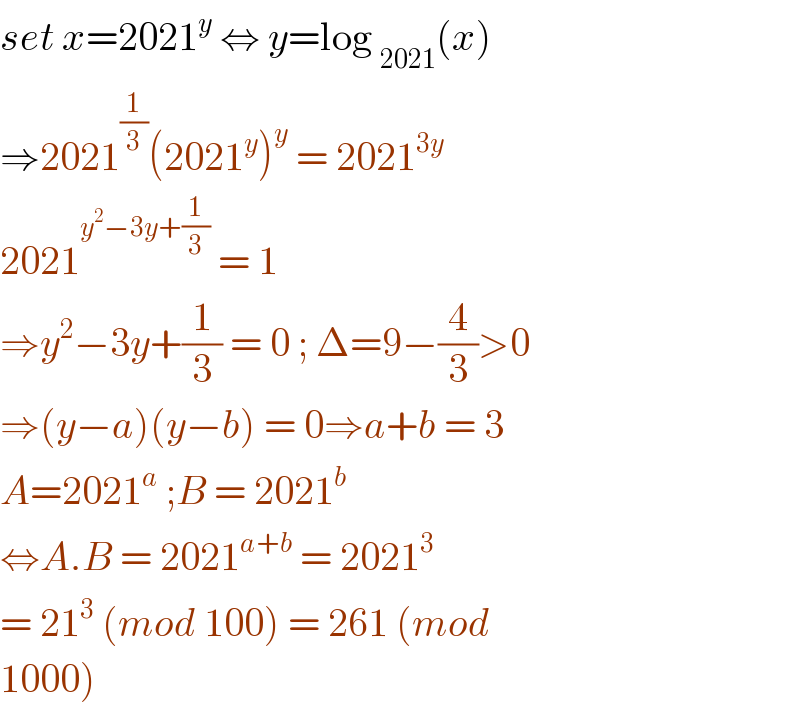
$${set}\:{x}=\mathrm{2021}^{{y}} \:\Leftrightarrow\:{y}=\mathrm{log}\:_{\mathrm{2021}} \left({x}\right) \\ $$$$\Rightarrow\mathrm{2021}^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{2021}^{{y}} \right)^{{y}} \:=\:\mathrm{2021}^{\mathrm{3}{y}} \\ $$$$\mathrm{2021}^{{y}^{\mathrm{2}} −\mathrm{3}{y}+\frac{\mathrm{1}}{\mathrm{3}}} \:=\:\mathrm{1}\: \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\mathrm{3}{y}+\frac{\mathrm{1}}{\mathrm{3}}\:=\:\mathrm{0}\:;\:\Delta=\mathrm{9}−\frac{\mathrm{4}}{\mathrm{3}}>\mathrm{0}\: \\ $$$$\Rightarrow\left({y}−{a}\right)\left({y}−{b}\right)\:=\:\mathrm{0}\Rightarrow{a}+{b}\:=\:\mathrm{3} \\ $$$${A}=\mathrm{2021}^{{a}} \:;{B}\:=\:\mathrm{2021}^{{b}} \\ $$$$\Leftrightarrow{A}.{B}\:=\:\mathrm{2021}^{{a}+{b}} \:=\:\mathrm{2021}^{\mathrm{3}} \\ $$$$=\:\mathrm{21}^{\mathrm{3}} \:\left({mod}\:\mathrm{100}\right)\:=\:\mathrm{261}\:\left({mod}\right. \\ $$$$\left.\mathrm{1000}\right) \\ $$
