Question Number 103072 by mr W last updated on 12/Jul/20

Commented by ajfour last updated on 12/Jul/20

Commented by mr W last updated on 12/Jul/20

$${a}\:{wedge}\:{with}\:{mass}\:{M}\:{has}\:{the}\:{shape} \\ $$$${of}\:{a}\:{quadrant}.\:{a}\:{small}\:{block}\:{with} \\ $$$${mass}\:{m}\:{is}\:{released}\:{at}\:{the}\:{top}\:{of}\:{the} \\ $$$${wedge}\:{as}\:{shown}\:{and}\:{can}\:{slide}\:{down} \\ $$$${frictionlessly}. \\ $$$${find}\:{the}\:{velocity}\:{of}\:{both}\:{objects}\:{at}\:{the} \\ $$$${instant}\:{when}\:{the}\:{small}\:{block}\:{leaves} \\ $$$${the}\:{wedge}. \\ $$$$\left({the}\:{friction}\:{between}\:{wedge}\:{and}\:\right. \\ $$$${ground}\:{is}\:{small}\:{enough}\:{so}\:{that}\:{the} \\ $$$$\left.{wedge}\:{can}\:{always}\:{move}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 12/Jul/20
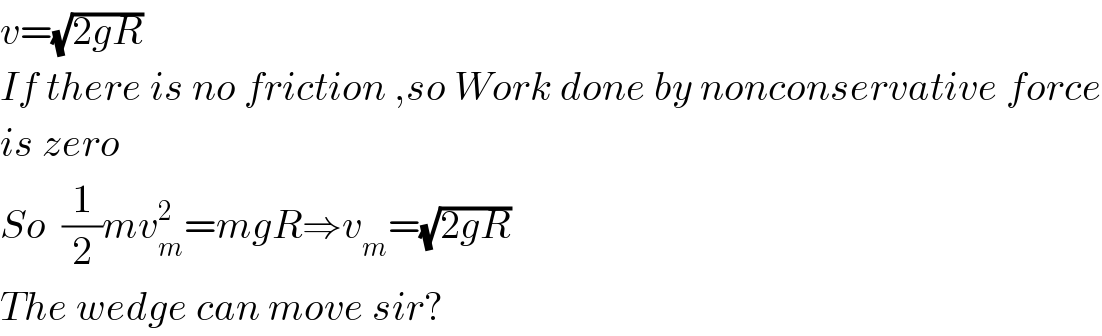
$${v}=\sqrt{\mathrm{2}{gR}} \\ $$$${If}\:{there}\:{is}\:{no}\:{friction}\:,{so}\:{Work}\:{done}\:{by}\:{nonconservative}\:{force} \\ $$$${is}\:{zero} \\ $$$${So}\:\:\frac{\mathrm{1}}{\mathrm{2}}{mv}_{{m}} ^{\mathrm{2}} ={mgR}\Rightarrow{v}_{{m}} =\sqrt{\mathrm{2}{gR}} \\ $$$${The}\:{wedge}\:{can}\:{move}\:{sir}? \\ $$
Commented by mr W last updated on 12/Jul/20
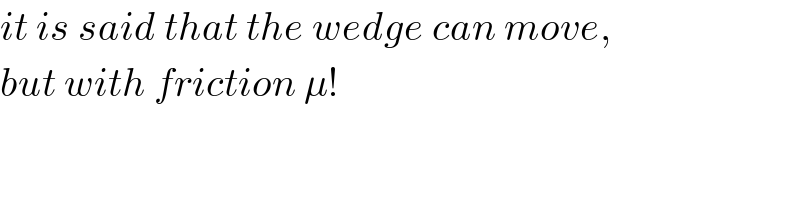
$${it}\:{is}\:{said}\:{that}\:{the}\:{wedge}\:{can}\:{move}, \\ $$$${but}\:{with}\:{friction}\:\mu! \\ $$
Commented by ajfour last updated on 13/Jul/20
![let radius of quadrant be r. System: Wedge_(−) Nsin θ+Mg=R ......(i) Ncos θ−μR=mA .......(ii) block (relative to wedge):_(−) mAcos θ+N−mgsin θ=((mu^2 )/r) (iii) mAsin θ+mgcos θ=((mudu)/(rdθ)) ..(iv) ________________________ from (i) & (ii) N(cos θ−μsin θ)−μMg=mA now using (iii) (mgsin θ+((mu^2 )/r)−mAcos θ)× (cos θ−μsin θ)−μMg=mA ⇒ A=(((cos θ−μsin θ)(gsin θ+(u^2 /r))−μ((M/m))g)/(1+cos θ(cos θ−μsin θ))) substituting this in (iv) ((udu)/(rdθ))=(([(cos θ−μsin θ)(gsin θ+(u^2 /r))−μ((M/m))g]sin θ)/(1+cos θ(cos θ−μsin θ))) +gcos θ If we are able to solve this D.E. we get u(θ). Let (u^2 /(rg))=t ; sin θ=s ⇒ ((udu)/(rg))=(dt/2) & cos θdθ=ds (1/2)(dt/ds)=((t[(1−((μs)/( (√(s^2 +1)))))(s+t)−μ((M/m))])/((1−s^2 −((μs)/(s^2 +1)))))+1 then we obtain A(θ) then V(θ) and v(θ) we then set θ=(π/2) , angular position of block when it leaves contact with wedge; (for m≪M)](https://www.tinkutara.com/question/Q103104.png)
$${let}\:{radius}\:{of}\:{quadrant}\:{be}\:\boldsymbol{{r}}. \\ $$$$\underset{−} {{System}:\:{Wedge}} \\ $$$${N}\mathrm{sin}\:\theta+{Mg}={R}\:\:\:\:\:\:\:……\left({i}\right) \\ $$$${N}\mathrm{cos}\:\theta−\mu{R}={mA}\:\:\:…….\left({ii}\right) \\ $$$$\underset{−} {{block}\:\left({relative}\:{to}\:{wedge}\right):} \\ $$$${mA}\mathrm{cos}\:\theta+{N}−{mg}\mathrm{sin}\:\theta=\frac{{mu}^{\mathrm{2}} }{{r}}\:\:\:\left({iii}\right) \\ $$$${mA}\mathrm{sin}\:\theta+{mg}\mathrm{cos}\:\theta=\frac{{mudu}}{{rd}\theta}\:\:\:\:\:..\left({iv}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${from}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$${N}\left(\mathrm{cos}\:\theta−\mu\mathrm{sin}\:\theta\right)−\mu{Mg}={mA} \\ $$$${now}\:{using}\:\left({iii}\right) \\ $$$$\left({mg}\mathrm{sin}\:\theta+\frac{{mu}^{\mathrm{2}} }{{r}}−{mA}\mathrm{cos}\:\theta\right)× \\ $$$$\left(\mathrm{cos}\:\theta−\mu\mathrm{sin}\:\theta\right)−\mu{Mg}={mA} \\ $$$$\Rightarrow \\ $$$${A}=\frac{\left(\mathrm{cos}\:\theta−\mu\mathrm{sin}\:\theta\right)\left({g}\mathrm{sin}\:\theta+\frac{{u}^{\mathrm{2}} }{{r}}\right)−\mu\left(\frac{{M}}{{m}}\right){g}}{\mathrm{1}+\mathrm{cos}\:\theta\left(\mathrm{cos}\:\theta−\mu\mathrm{sin}\:\theta\right)} \\ $$$${substituting}\:{this}\:{in}\:\left({iv}\right) \\ $$$$\frac{{udu}}{{rd}\theta}=\frac{\left[\left(\mathrm{cos}\:\theta−\mu\mathrm{sin}\:\theta\right)\left({g}\mathrm{sin}\:\theta+\frac{{u}^{\mathrm{2}} }{{r}}\right)−\mu\left(\frac{{M}}{{m}}\right){g}\right]\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta\left(\mathrm{cos}\:\theta−\mu\mathrm{sin}\:\theta\right)} \\ $$$$\:\:\:\:\:\:\:\:+{g}\mathrm{cos}\:\theta \\ $$$${If}\:{we}\:{are}\:{able}\:{to}\:{solve}\:{this}\:{D}.{E}. \\ $$$${we}\:{get}\:{u}\left(\theta\right). \\ $$$${Let}\:\:\:\frac{{u}^{\mathrm{2}} }{{rg}}={t}\:\:\:;\:\:\mathrm{sin}\:\theta={s} \\ $$$$\Rightarrow\:\:\frac{{udu}}{{rg}}=\frac{{dt}}{\mathrm{2}}\:\:\:\&\:\:\:\mathrm{cos}\:\theta{d}\theta={ds} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\frac{{dt}}{{ds}}=\frac{{t}\left[\left(\mathrm{1}−\frac{\mu{s}}{\:\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}}\right)\left({s}+{t}\right)−\mu\left(\frac{{M}}{{m}}\right)\right]}{\left(\mathrm{1}−{s}^{\mathrm{2}} −\frac{\mu{s}}{{s}^{\mathrm{2}} +\mathrm{1}}\right)}+\mathrm{1} \\ $$$${then}\:{we}\:{obtain}\:{A}\left(\theta\right) \\ $$$${then}\:\:{V}\left(\theta\right)\:\:\:{and}\:\:{v}\left(\theta\right) \\ $$$${we}\:{then}\:{set}\:\:\:\theta=\frac{\pi}{\mathrm{2}}\:,\:\:\:{angular} \\ $$$${position}\:{of}\:{block}\:{when}\:{it}\:{leaves} \\ $$$${contact}\:{with}\:{wedge};\: \\ $$$$\left({for}\:{m}\ll{M}\right) \\ $$
Commented by mr W last updated on 12/Jul/20
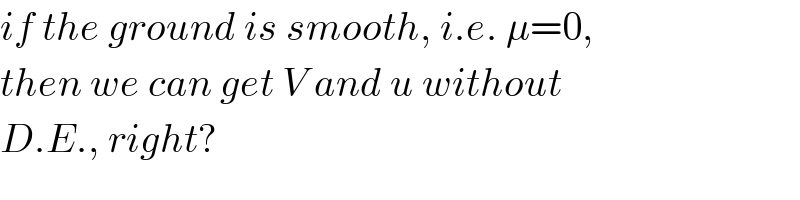
$${if}\:{the}\:{ground}\:{is}\:{smooth},\:{i}.{e}.\:\mu=\mathrm{0}, \\ $$$${then}\:{we}\:{can}\:{get}\:{V}\:{and}\:{u}\:{without} \\ $$$${D}.{E}.,\:{right}? \\ $$
Commented by ajfour last updated on 12/Jul/20

$${the}\:{diff}.\:{eq}.\:{would}\:{be}\:{much} \\ $$$${simpler}\:{then}\:{Sir}…. \\ $$
Commented by mr W last updated on 12/Jul/20

$${that}'{s}\:{true}… \\ $$
Commented by mr W last updated on 12/Jul/20

$${if}\:{we}\:{only}\:{want}\:{to}\:{determine}\:{the} \\ $$$${velocities}\:{V}\:{and}\:{u},\:{we}\:{don}'{t}\:{need}\:{to} \\ $$$${solve}\:{the}\:{D}.{E}.,\:{because}\:{we}\:{have} \\ $$$${MV}={mu}_{{x}} . \\ $$
Answered by ajfour last updated on 13/Jul/20
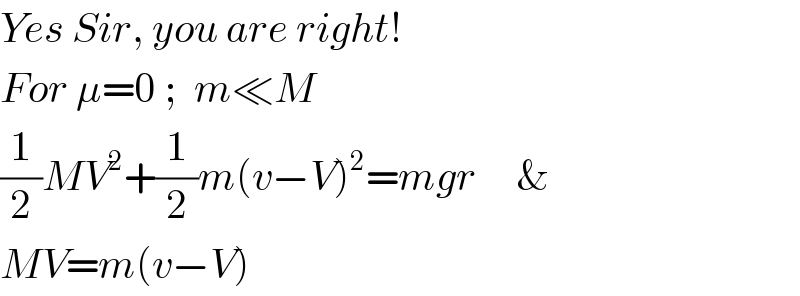
$${Yes}\:{Sir},\:{you}\:{are}\:{right}! \\ $$$${For}\:\mu=\mathrm{0}\:;\:\:{m}\ll{M} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{MV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}\left({v}−{V}\right)^{\mathrm{2}} ={mgr}\:\:\:\:\:\& \\ $$$${MV}={m}\left({v}−{V}\right) \\ $$
