Menu Close

solve-for-x-y-N-1-x-1-y-3-202-

Tinku Tara 0 Comments
Pin




Question Number 103093 by mr W last updated on 12/Jul/20
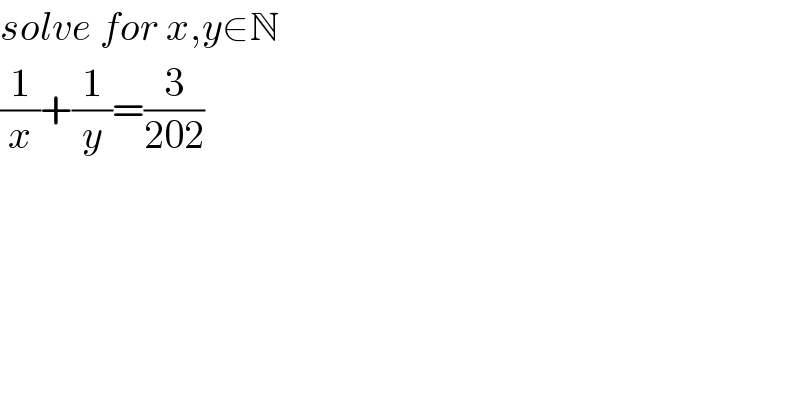
solve for x,y∈N (1/x)+(1/y)=(3/(202))
$${solve}\:{for}\:{x},{y}\in\mathbb{N} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{3}}{\mathrm{202}} \\ $$
Answered by 1549442205 last updated on 13/Jul/20
We have (1/x)+(1/y)=(3/(202))⇔((x+y)/(xy))=(3/(202)) ⇔3xy=202(x+y)⇔9xy=3.202(x+y) ⇔(3x−202)(3y−202)=202^2 ⇒3x−202∣202^2 =101^2 ×2^2 ⇒3x−202∈{1,2,4,101,202,404,10201,20402,40804} The case 1,4,202,10201,40804 is reject because when plus to 202 we obtain a number which isn′t divisible by 3. We have following tables: determinant (((3x−202),2,(101),(404),(20402)),((3y−202),(202×101),(101×4),(101),2),(x,(68),(101),(202),(6868)),(y,(6868),(202),(101),(68))) Thus,the set of solutions as {(68;6868);(101;202);(202;101);(6868;68)}
$$\mathrm{We}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{3}}{\mathrm{202}}\Leftrightarrow\frac{\mathrm{x}+\mathrm{y}}{\mathrm{xy}}=\frac{\mathrm{3}}{\mathrm{202}} \\ $$$$\Leftrightarrow\mathrm{3xy}=\mathrm{202}\left(\mathrm{x}+\mathrm{y}\right)\Leftrightarrow\mathrm{9xy}=\mathrm{3}.\mathrm{202}\left(\mathrm{x}+\mathrm{y}\right) \\ $$$$\Leftrightarrow\left(\mathrm{3x}−\mathrm{202}\right)\left(\mathrm{3y}−\mathrm{202}\right)=\mathrm{202}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{3x}−\mathrm{202}\mid\mathrm{202}^{\mathrm{2}} =\mathrm{101}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{3x}−\mathrm{202}\in\left\{\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{101},\mathrm{202},\mathrm{404},\mathrm{10201},\mathrm{20402},\mathrm{40804}\right\} \\ $$$$\mathrm{The}\:\mathrm{case}\:\mathrm{1},\mathrm{4},\mathrm{202},\mathrm{10201},\mathrm{40804}\:\mathrm{is}\:\mathrm{reject} \\ $$$$\mathrm{because}\:\mathrm{when}\:\:\mathrm{plus}\:\mathrm{to}\:\mathrm{202}\:\mathrm{we}\:\mathrm{obtain} \\ $$$$\mathrm{a}\:\mathrm{number}\:\mathrm{which}\:\mathrm{isn}'\mathrm{t}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3}. \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{following}\:\mathrm{tables}: \\ $$$$\begin{vmatrix}{\mathrm{3x}−\mathrm{202}}&{\mathrm{2}}&{\mathrm{101}}&{\mathrm{404}}&{\mathrm{20402}}\\{\mathrm{3y}−\mathrm{202}}&{\mathrm{202}×\mathrm{101}}&{\mathrm{101}×\mathrm{4}}&{\mathrm{101}}&{\mathrm{2}}\\{\mathrm{x}}&{\mathrm{68}}&{\mathrm{101}}&{\mathrm{202}}&{\mathrm{6868}}\\{\mathrm{y}}&{\mathrm{6868}}&{\mathrm{202}}&{\mathrm{101}}&{\mathrm{68}}\end{vmatrix} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\:\mathrm{solutions}\:\mathrm{as} \\ $$$$\left\{\left(\mathrm{68};\mathrm{6868}\right);\left(\mathrm{101};\mathrm{202}\right);\left(\mathrm{202};\mathrm{101}\right);\left(\mathrm{6868};\mathrm{68}\right)\right\} \\ $$$$ \\ $$
Commented by mr W last updated on 13/Jul/20
thanks sir!
$${thanks}\:{sir}! \\ $$
Answered by Rasheed.Sindhi last updated on 13/Jul/20
((x+y)/(xy))=(3/(202)) x+y=3k ∧ xy=202k xy=1×2×101×k possible values for x(or y): x=1,2,101,202,k,2k,101k,202k y=((202k)/x)=202k,101k,2k,k,202,101,2,1 y=3k−x=3k−1,3k−2,3k−101,3k−202, determinant ((x,( y),( y),( k),x,y),(,(=(202k)/x),(=3k−x),,,),(1,(202k),(3k−1),(−1/199),1,−),(2,(101k),(3k−2),(−1/49),2,−),((101),(2k),(3k−101),(101),(101),(202)),((202),k,(3k−202),(101),(202),(101)),(k,(202),(2k),(101),(101),(202)),((2k),(101),k,(101),(202),(101)),((101k),2,(−98k),(−1/49),−,2),((202k),1,(−199k),(−1/199),−,1)) x=k ((k+y)/(ky))=(3/(202)) y=((202k)/(3k−202)) 3k−202=1,2,101,202,k,2k,101k,202k 3k−202=k,2k,101k,202k (in general) k=101,202,((−101)/(49)),((−202)/(199)) y=202,101 x=101,202 (_★ ^★ ) x=2k ((2k+y)/(2ky))=(3/(202)) 404k+202y=6ky y=((202k)/(3k−101)) 3k−101=1,2,101,202,k,2k,101k,202k 3k−101=k,2k,101k,202k(in general) k=((101)/2),101,((−101)/(98)),((−101)/(199)) for k=101 y=202 x=101 3k−101=1⇒k=34⇒y=6868 3k−101=2k⇒k=101⇒y=101 3k−101=101k⇒y∉N 3k−101=202k⇒y∉N y=101k .... y=202k .......
$$\frac{{x}+{y}}{{xy}}=\frac{\mathrm{3}}{\mathrm{202}} \\ $$$${x}+{y}=\mathrm{3}{k}\:\wedge\:{xy}=\mathrm{202}{k} \\ $$$$\:\:\:\:\:\:\:\:{xy}=\mathrm{1}×\mathrm{2}×\mathrm{101}×{k} \\ $$$${possible}\:{values}\:{for}\:{x}\left({or}\:{y}\right): \\ $$$${x}=\mathrm{1},\mathrm{2},\mathrm{101},\mathrm{202},{k},\mathrm{2}{k},\mathrm{101}{k},\mathrm{202}{k} \\ $$$${y}=\frac{\mathrm{202}{k}}{{x}}=\mathrm{202}{k},\mathrm{101}{k},\mathrm{2}{k},{k},\mathrm{202},\mathrm{101},\mathrm{2},\mathrm{1} \\ $$$${y}=\mathrm{3}{k}−{x}=\mathrm{3}{k}−\mathrm{1},\mathrm{3}{k}−\mathrm{2},\mathrm{3}{k}−\mathrm{101},\mathrm{3}{k}−\mathrm{202}, \\ $$$$\begin{vmatrix}{{x}}&{\:\:\:\:\:\:\:\:\:\:{y}}&{\:\:\:\:\:\:\:{y}}&{\:\:\:\:\:\:\:{k}}&{{x}}&{{y}}\\{}&{=\left(\mathrm{202}{k}\right)/{x}}&{=\mathrm{3}{k}−{x}}&{}&{}&{}\\{\mathrm{1}}&{\mathrm{202}{k}}&{\mathrm{3}{k}−\mathrm{1}}&{−\mathrm{1}/\mathrm{199}}&{\mathrm{1}}&{−}\\{\mathrm{2}}&{\mathrm{101}{k}}&{\mathrm{3}{k}−\mathrm{2}}&{−\mathrm{1}/\mathrm{49}}&{\mathrm{2}}&{−}\\{\mathrm{101}}&{\mathrm{2}{k}}&{\mathrm{3}{k}−\mathrm{101}}&{\mathrm{101}}&{\mathrm{101}}&{\mathrm{202}}\\{\mathrm{202}}&{{k}}&{\mathrm{3}{k}−\mathrm{202}}&{\mathrm{101}}&{\mathrm{202}}&{\mathrm{101}}\\{{k}}&{\mathrm{202}}&{\mathrm{2}{k}}&{\mathrm{101}}&{\mathrm{101}}&{\mathrm{202}}\\{\mathrm{2}{k}}&{\mathrm{101}}&{{k}}&{\mathrm{101}}&{\mathrm{202}}&{\mathrm{101}}\\{\mathrm{101}{k}}&{\mathrm{2}}&{−\mathrm{98}{k}}&{−\mathrm{1}/\mathrm{49}}&{−}&{\mathrm{2}}\\{\mathrm{202}{k}}&{\mathrm{1}}&{−\mathrm{199}{k}}&{−\mathrm{1}/\mathrm{199}}&{−}&{\mathrm{1}}\end{vmatrix} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$${x}={k} \\ $$$$\frac{{k}+{y}}{{ky}}=\frac{\mathrm{3}}{\mathrm{202}} \\ $$$${y}=\frac{\mathrm{202}{k}}{\mathrm{3}{k}−\mathrm{202}} \\ $$$$\mathrm{3}{k}−\mathrm{202}=\mathrm{1},\mathrm{2},\mathrm{101},\mathrm{202},{k},\mathrm{2}{k},\mathrm{101}{k},\mathrm{202}{k} \\ $$$$\mathrm{3}{k}−\mathrm{202}={k},\mathrm{2}{k},\mathrm{101}{k},\mathrm{202}{k}\:\left({in}\:{general}\right) \\ $$$${k}=\mathrm{101},\mathrm{202},\frac{−\mathrm{101}}{\mathrm{49}},\frac{−\mathrm{202}}{\mathrm{199}} \\ $$$${y}=\mathrm{202},\mathrm{101} \\ $$$${x}=\mathrm{101},\mathrm{202}\:\:\left(_{\bigstar} ^{\bigstar} \right) \\ $$$${x}=\mathrm{2}{k} \\ $$$$\frac{\mathrm{2}{k}+{y}}{\mathrm{2}{ky}}=\frac{\mathrm{3}}{\mathrm{202}} \\ $$$$\mathrm{404}{k}+\mathrm{202}{y}=\mathrm{6}{ky} \\ $$$${y}=\frac{\mathrm{202}{k}}{\mathrm{3}{k}−\mathrm{101}} \\ $$$$\mathrm{3}{k}−\mathrm{101}=\mathrm{1},\mathrm{2},\mathrm{101},\mathrm{202},{k},\mathrm{2}{k},\mathrm{101}{k},\mathrm{202}{k} \\ $$$$\mathrm{3}{k}−\mathrm{101}={k},\mathrm{2}{k},\mathrm{101}{k},\mathrm{202}{k}\left({in}\:{general}\right) \\ $$$${k}=\frac{\mathrm{101}}{\mathrm{2}},\mathrm{101},\frac{−\mathrm{101}}{\mathrm{98}},\frac{−\mathrm{101}}{\mathrm{199}} \\ $$$${for}\:{k}=\mathrm{101} \\ $$$${y}=\mathrm{202} \\ $$$${x}=\mathrm{101} \\ $$$$\mathrm{3}{k}−\mathrm{101}=\mathrm{1}\Rightarrow{k}=\mathrm{34}\Rightarrow{y}=\mathrm{6868} \\ $$$$\mathrm{3}{k}−\mathrm{101}=\mathrm{2}{k}\Rightarrow{k}=\mathrm{101}\Rightarrow{y}=\mathrm{101} \\ $$$$\mathrm{3}{k}−\mathrm{101}=\mathrm{101}{k}\Rightarrow{y}\notin\mathbb{N} \\ $$$$\mathrm{3}{k}−\mathrm{101}=\mathrm{202}{k}\Rightarrow{y}\notin\mathbb{N} \\ $$$$ \\ $$$${y}=\mathrm{101}{k} \\ $$$$…. \\ $$$${y}=\mathrm{202}{k} \\ $$$$……. \\ $$
Commented by Dwaipayan Shikari last updated on 12/Jul/20
There is an another solution( 68,6868) or (6868,68) ∈N
$${There}\:{is}\:{an}\:{another}\:{solution}\left(\:\mathrm{68},\mathrm{6868}\right)\:{or}\:\left(\mathrm{6868},\mathrm{68}\right)\:\:\in\mathbb{N} \\ $$
Commented by mr W last updated on 12/Jul/20
how did you get it and how are you sure that no other solutions exist?
$${how}\:{did}\:{you}\:{get}\:{it}\:{and}\:{how}\:{are}\:{you} \\ $$$${sure}\:{that}\:{no}\:{other}\:{solutions}\:{exist}? \\ $$
Answered by nimnim last updated on 12/Jul/20
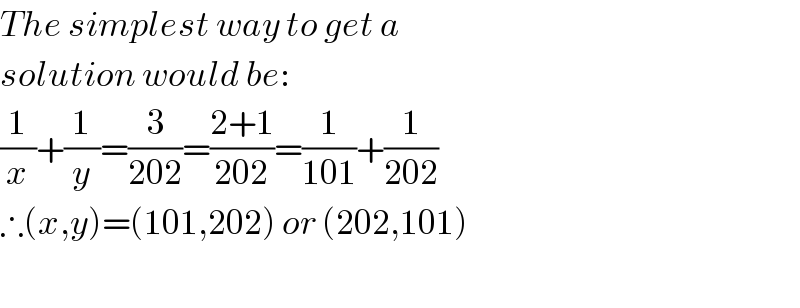
The simplest way to get a solution would be: (1/x)+(1/y)=(3/(202))=((2+1)/(202))=(1/(101))+(1/(202)) ∴(x,y)=(101,202) or (202,101)
$${The}\:{simplest}\:{way}\:{to}\:{get}\:{a}\: \\ $$$${solution}\:{would}\:{be}: \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{3}}{\mathrm{202}}=\frac{\mathrm{2}+\mathrm{1}}{\mathrm{202}}=\frac{\mathrm{1}}{\mathrm{101}}+\frac{\mathrm{1}}{\mathrm{202}} \\ $$$$\therefore\left({x},{y}\right)=\left(\mathrm{101},\mathrm{202}\right)\:{or}\:\left(\mathrm{202},\mathrm{101}\right) \\ $$$$ \\ $$
Commented by mr W last updated on 12/Jul/20
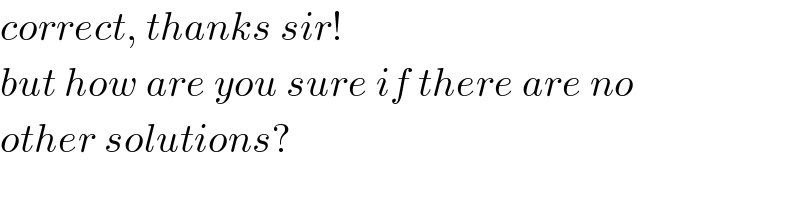
correct, thanks sir! but how are you sure if there are no other solutions?
$${correct},\:{thanks}\:{sir}! \\ $$$${but}\:{how}\:{are}\:{you}\:{sure}\:{if}\:{there}\:{are}\:{no} \\ $$$${other}\:{solutions}? \\ $$
Answered by floor(10²Eta[1]) last updated on 12/Jul/20
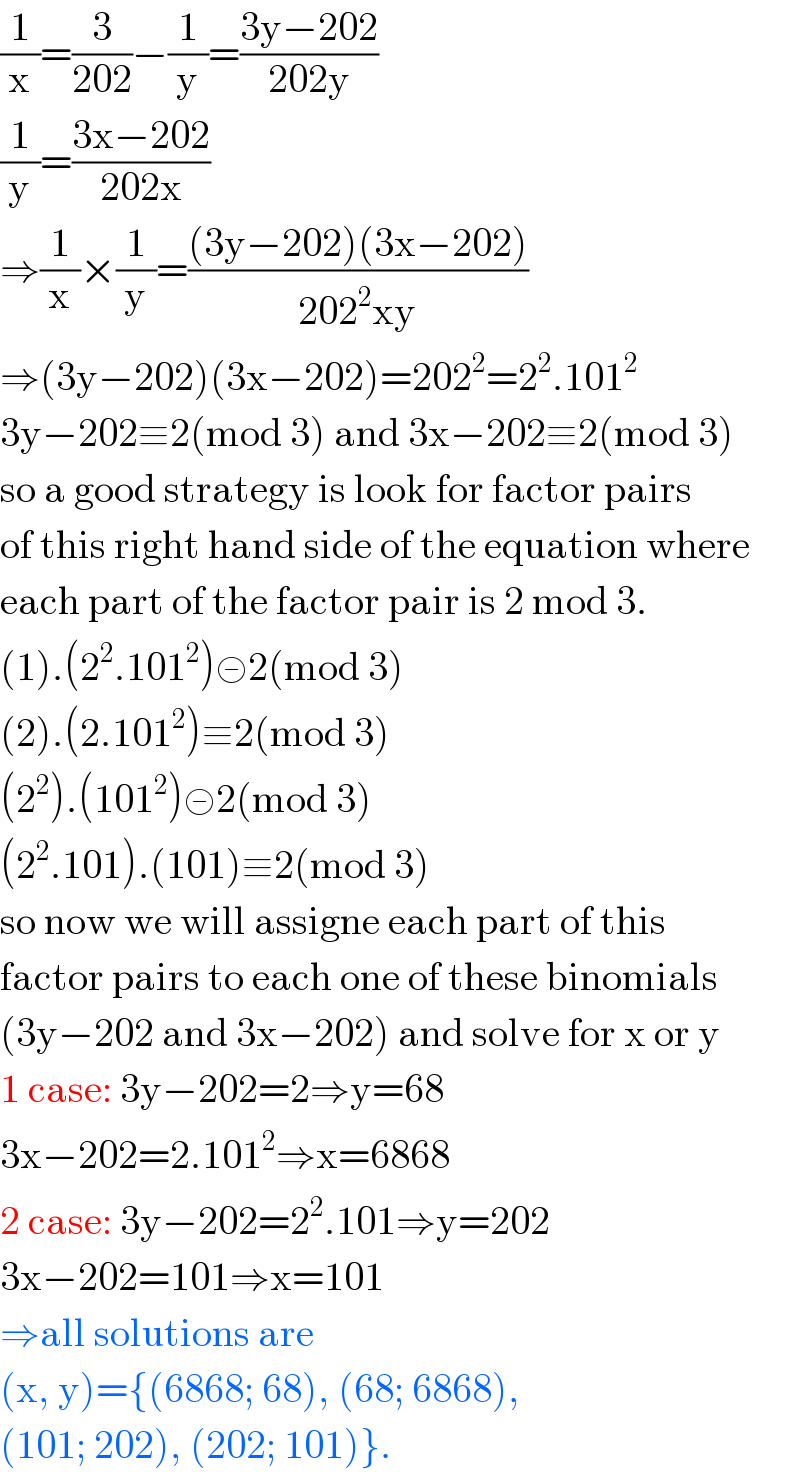
(1/x)=(3/(202))−(1/y)=((3y−202)/(202y)) (1/y)=((3x−202)/(202x)) ⇒(1/x)×(1/y)=(((3y−202)(3x−202))/(202^2 xy)) ⇒(3y−202)(3x−202)=202^2 =2^2 .101^2 3y−202≡2(mod 3) and 3x−202≡2(mod 3) so a good strategy is look for factor pairs of this right hand side of the equation where each part of the factor pair is 2 mod 3. (1).(2^2 .101^2 )≢2(mod 3) (2).(2.101^2 )≡2(mod 3) (2^2 ).(101^2 )≢2(mod 3) (2^2 .101).(101)≡2(mod 3) so now we will assigne each part of this factor pairs to each one of these binomials (3y−202 and 3x−202) and solve for x or y 1 case: 3y−202=2⇒y=68 3x−202=2.101^2 ⇒x=6868 2 case: 3y−202=2^2 .101⇒y=202 3x−202=101⇒x=101 ⇒all solutions are (x, y)={(6868; 68), (68; 6868), (101; 202), (202; 101)}.
$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{3}}{\mathrm{202}}−\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{3y}−\mathrm{202}}{\mathrm{202y}} \\ $$$$\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{3x}−\mathrm{202}}{\mathrm{202x}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{x}}×\frac{\mathrm{1}}{\mathrm{y}}=\frac{\left(\mathrm{3y}−\mathrm{202}\right)\left(\mathrm{3x}−\mathrm{202}\right)}{\mathrm{202}^{\mathrm{2}} \mathrm{xy}} \\ $$$$\Rightarrow\left(\mathrm{3y}−\mathrm{202}\right)\left(\mathrm{3x}−\mathrm{202}\right)=\mathrm{202}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} .\mathrm{101}^{\mathrm{2}} \\ $$$$\mathrm{3y}−\mathrm{202}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{3}\right)\:\mathrm{and}\:\mathrm{3x}−\mathrm{202}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\mathrm{so}\:\mathrm{a}\:\mathrm{good}\:\mathrm{strategy}\:\mathrm{is}\:\mathrm{look}\:\mathrm{for}\:\mathrm{factor}\:\mathrm{pairs} \\ $$$$\mathrm{of}\:\mathrm{this}\:\mathrm{right}\:\mathrm{hand}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{where} \\ $$$$\mathrm{each}\:\mathrm{part}\:\mathrm{of}\:\mathrm{the}\:\mathrm{factor}\:\mathrm{pair}\:\mathrm{is}\:\mathrm{2}\:\mathrm{mod}\:\mathrm{3}. \\ $$$$\left(\mathrm{1}\right).\left(\mathrm{2}^{\mathrm{2}} .\mathrm{101}^{\mathrm{2}} \right)≢\mathrm{2}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right).\left(\mathrm{2}.\mathrm{101}^{\mathrm{2}} \right)\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\left(\mathrm{2}^{\mathrm{2}} \right).\left(\mathrm{101}^{\mathrm{2}} \right)≢\mathrm{2}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\left(\mathrm{2}^{\mathrm{2}} .\mathrm{101}\right).\left(\mathrm{101}\right)\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\mathrm{so}\:\mathrm{now}\:\mathrm{we}\:\mathrm{will}\:\mathrm{assigne}\:\mathrm{each}\:\mathrm{part}\:\mathrm{of}\:\mathrm{this} \\ $$$$\mathrm{factor}\:\mathrm{pairs}\:\mathrm{to}\:\mathrm{each}\:\mathrm{one}\:\mathrm{of}\:\mathrm{these}\:\mathrm{binomials} \\ $$$$\left(\mathrm{3y}−\mathrm{202}\:\mathrm{and}\:\mathrm{3x}−\mathrm{202}\right)\:\mathrm{and}\:\mathrm{solve}\:\mathrm{for}\:\mathrm{x}\:\mathrm{or}\:\mathrm{y} \\ $$$$\mathrm{1}\:\mathrm{case}:\:\mathrm{3y}−\mathrm{202}=\mathrm{2}\Rightarrow\mathrm{y}=\mathrm{68} \\ $$$$\mathrm{3x}−\mathrm{202}=\mathrm{2}.\mathrm{101}^{\mathrm{2}} \Rightarrow\mathrm{x}=\mathrm{6868} \\ $$$$\mathrm{2}\:\mathrm{case}:\:\mathrm{3y}−\mathrm{202}=\mathrm{2}^{\mathrm{2}} .\mathrm{101}\Rightarrow\mathrm{y}=\mathrm{202} \\ $$$$\mathrm{3x}−\mathrm{202}=\mathrm{101}\Rightarrow\mathrm{x}=\mathrm{101} \\ $$$$\Rightarrow\mathrm{all}\:\mathrm{solutions}\:\mathrm{are}\: \\ $$$$\left(\mathrm{x},\:\mathrm{y}\right)=\left\{\left(\mathrm{6868};\:\mathrm{68}\right),\:\left(\mathrm{68};\:\mathrm{6868}\right),\:\right. \\ $$$$\left.\left(\mathrm{101};\:\mathrm{202}\right),\:\left(\mathrm{202};\:\mathrm{101}\right)\right\}. \\ $$
Commented by mr W last updated on 12/Jul/20
thanks alot sir!
$${thanks}\:{alot}\:{sir}! \\ $$
Answered by Rasheed.Sindhi last updated on 14/Jul/20
An Easy ∧ Short approach (1/y)=(3/(202))−(1/x)=((3x−202)/(202x)) y=((202x)/(3x−202))⇒3x−202 ∣ 202x possible values for 3x−202 _(−) 3x−202=1,2,101,202,x,2x,101x,202x determinant (((3x−202=),( x),( y)),(( 1),(((1+202)/3)=((203)/3)∉N),( −)),(( 2),(((2+202)/3)=68),(6868)),(( 101),(((101+202)/3)=101),( 202)),(( 202),(((202+202)/3)=((404)/3)∉N),( −)),(( x),(2x=202⇒x=101),( 202)),(( 2x),(x=202),( 101)),(( 101x),(98x=−202⇒x∉N),( −)),(( 202x),(199x=−202⇒x∉N),( −)))
$$\mathcal{A}{n}\:\mathcal{E}{asy}\:\wedge\:\mathcal{S}{hort}\:{approach} \\ $$$$\frac{\mathrm{1}}{{y}}=\frac{\mathrm{3}}{\mathrm{202}}−\frac{\mathrm{1}}{{x}}=\frac{\mathrm{3}{x}−\mathrm{202}}{\mathrm{202}{x}} \\ $$$$\:\:\:{y}=\frac{\mathrm{202}{x}}{\mathrm{3}{x}−\mathrm{202}}\Rightarrow\mathrm{3}{x}−\mathrm{202}\:\mid\:\mathrm{202}{x} \\ $$$$\underset{−} {\:\:{possible}\:{values}\:{for}\:\mathrm{3}{x}−\mathrm{202}\:\:\:} \\ $$$$\mathrm{3}{x}−\mathrm{202}=\mathrm{1},\mathrm{2},\mathrm{101},\mathrm{202},{x},\mathrm{2}{x},\mathrm{101}{x},\mathrm{202}{x} \\ $$$$\begin{vmatrix}{\mathrm{3}{x}−\mathrm{202}=}&{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}}&{\:\:\:{y}}\\{\:\:\:\:\:\:\:\:\:\mathrm{1}}&{\frac{\mathrm{1}+\mathrm{202}}{\mathrm{3}}=\frac{\mathrm{203}}{\mathrm{3}}\notin\mathbb{N}}&{\:−}\\{\:\:\:\:\:\:\:\:\:\mathrm{2}}&{\frac{\mathrm{2}+\mathrm{202}}{\mathrm{3}}=\mathrm{68}}&{\mathrm{6868}}\\{\:\:\:\:\:\:\mathrm{101}}&{\frac{\mathrm{101}+\mathrm{202}}{\mathrm{3}}=\mathrm{101}}&{\:\mathrm{202}}\\{\:\:\:\:\:\:\mathrm{202}}&{\frac{\mathrm{202}+\mathrm{202}}{\mathrm{3}}=\frac{\mathrm{404}}{\mathrm{3}}\notin\mathbb{N}}&{\:\:−}\\{\:\:\:\:\:\:\:\:{x}}&{\mathrm{2}{x}=\mathrm{202}\Rightarrow{x}=\mathrm{101}}&{\:\mathrm{202}}\\{\:\:\:\:\:\:\mathrm{2}{x}}&{{x}=\mathrm{202}}&{\:\mathrm{101}}\\{\:\:\:\:\mathrm{101}{x}}&{\mathrm{98}{x}=−\mathrm{202}\Rightarrow{x}\notin\mathbb{N}}&{\:\:−}\\{\:\:\:\:\mathrm{202}{x}}&{\mathrm{199}{x}=−\mathrm{202}\Rightarrow{x}\notin\mathbb{N}}&{\:\:−}\end{vmatrix} \\ $$
Commented by mr W last updated on 17/Jul/20
great! thanks alot!
$${great}!\:{thanks}\:{alot}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *