Question Number 103130 by chamkunda last updated on 13/Jul/20
![find out the fourth member of the following formula after expansion [πx+(2/x)]^8](https://www.tinkutara.com/question/Q103130.png)
$$ \\ $$$${find}\:{out}\:{the}\:{fourth}\:{member}\:{of}\:{the} \\ $$$${following}\:{formula}\:{after}\:{expansion} \\ $$$$\left[\pi{x}+\frac{\mathrm{2}}{{x}}\right]^{\mathrm{8}} \\ $$
Commented by chamkunda last updated on 13/Jul/20
![please can someone help and answer this find out the fourth member of the following formula after expansion [πx+(2/x)]^8 find out the fourth member of the following formula after expansion [πx+(2/x)]^8](https://www.tinkutara.com/question/Q103131.png)
$${please}\:{can}\:{someone}\:{help}\:{and}\:{answer}\:{this} \\ $$$${find}\:{out}\:{the}\:{fourth}\:{member}\:{of}\:{the} \\ $$$${following}\:{formula}\:{after}\:{expansion} \\ $$$$\left[\pi{x}+\frac{\mathrm{2}}{{x}}\right]^{\mathrm{8}} \\ $$$$ \\ $$$${find}\:{out}\:{the}\:{fourth}\:{member}\:{of}\:{the} \\ $$$${following}\:{formula}\:{after}\:{expansion} \\ $$$$\left[\pi{x}+\frac{\mathrm{2}}{{x}}\right]^{\mathrm{8}} \\ $$
Answered by floor(10²Eta[1]) last updated on 13/Jul/20
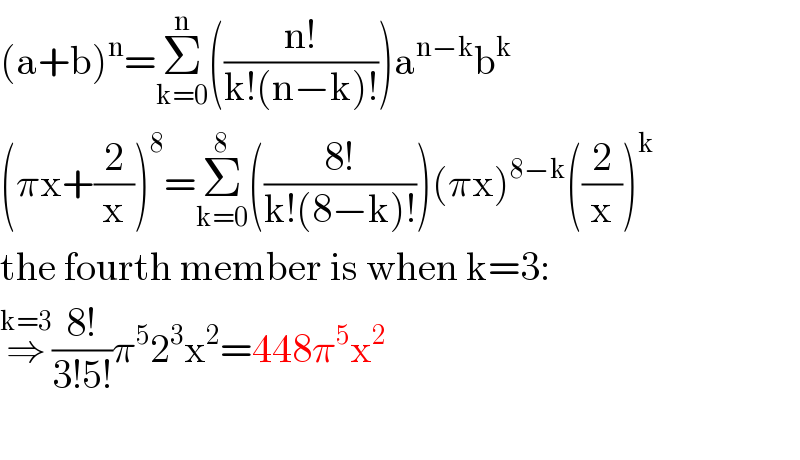
$$\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{n}!}{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!}\right)\mathrm{a}^{\mathrm{n}−\mathrm{k}} \mathrm{b}^{\mathrm{k}} \\ $$$$\left(\pi\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)^{\mathrm{8}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{8}} {\sum}}\left(\frac{\mathrm{8}!}{\mathrm{k}!\left(\mathrm{8}−\mathrm{k}\right)!}\right)\left(\pi\mathrm{x}\right)^{\mathrm{8}−\mathrm{k}} \left(\frac{\mathrm{2}}{\mathrm{x}}\right)^{\mathrm{k}} \\ $$$$\mathrm{the}\:\mathrm{fourth}\:\mathrm{member}\:\mathrm{is}\:\mathrm{when}\:\mathrm{k}=\mathrm{3}: \\ $$$$\overset{\mathrm{k}=\mathrm{3}} {\Rightarrow}\frac{\mathrm{8}!}{\mathrm{3}!\mathrm{5}!}\pi^{\mathrm{5}} \mathrm{2}^{\mathrm{3}} \mathrm{x}^{\mathrm{2}} =\mathrm{448}\pi^{\mathrm{5}} \mathrm{x}^{\mathrm{2}} \\ $$$$ \\ $$
Answered by bemath last updated on 13/Jul/20
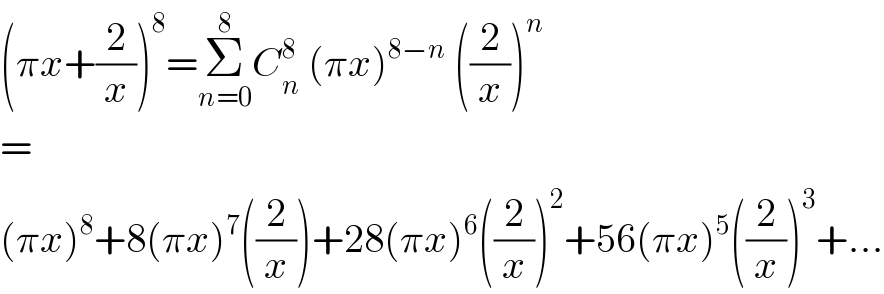
$$\left(\pi{x}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{8}} =\underset{{n}=\mathrm{0}} {\overset{\mathrm{8}} {\sum}}{C}_{{n}} ^{\mathrm{8}} \:\left(\pi{x}\right)^{\mathrm{8}−{n}} \:\left(\frac{\mathrm{2}}{{x}}\right)^{{n}} \\ $$$$= \\ $$$$\left(\pi{x}\right)^{\mathrm{8}} +\mathrm{8}\left(\pi{x}\right)^{\mathrm{7}} \left(\frac{\mathrm{2}}{{x}}\right)+\mathrm{28}\left(\pi{x}\right)^{\mathrm{6}} \left(\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} +\mathrm{56}\left(\pi{x}\right)^{\mathrm{5}} \left(\frac{\mathrm{2}}{{x}}\right)^{\mathrm{3}} +… \\ $$
Commented by 1549442205 last updated on 13/Jul/20

$$\mathrm{I}\:\mathrm{agree}\:\mathrm{to}\:\mathrm{this}\:\mathrm{expansion}\:\mathrm{a}_{\mathrm{3}} =\frac{\mathrm{8}!}{\mathrm{2}!\mathrm{6}!}\pi^{\mathrm{6}} \mathrm{x}^{\mathrm{6}} ×\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\mathrm{112}\boldsymbol{\pi}^{\mathrm{6}} \boldsymbol{\mathrm{x}}^{\mathrm{4}} ,\boldsymbol{\mathrm{excuse}}\:\boldsymbol{\mathrm{me}}\:\:\boldsymbol{\mathrm{a}}_{\mathrm{4}} =\mathrm{448}\boldsymbol{\pi}^{\mathrm{5}} \boldsymbol{\mathrm{x}}^{\mathrm{2}} \:\boldsymbol{\mathrm{as}} \\ $$$$\boldsymbol{\mathrm{above}} \\ $$
Commented by floor(10²Eta[1]) last updated on 13/Jul/20
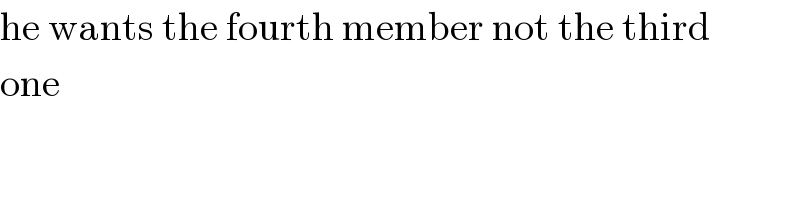
$$\mathrm{he}\:\mathrm{wants}\:\mathrm{the}\:\mathrm{fourth}\:\mathrm{member}\:\mathrm{not}\:\mathrm{the}\:\mathrm{third} \\ $$$$\mathrm{one} \\ $$
Answered by OlafThorendsen last updated on 13/Jul/20
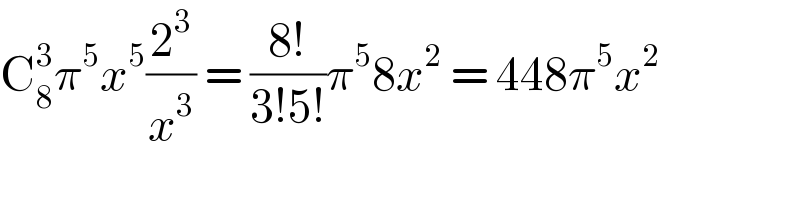
$$\mathrm{C}_{\mathrm{8}} ^{\mathrm{3}} \pi^{\mathrm{5}} {x}^{\mathrm{5}} \frac{\mathrm{2}^{\mathrm{3}} }{{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{8}!}{\mathrm{3}!\mathrm{5}!}\pi^{\mathrm{5}} \mathrm{8}{x}^{\mathrm{2}} \:=\:\mathrm{448}\pi^{\mathrm{5}} {x}^{\mathrm{2}} \\ $$
